백준 2110번 공유기 설치 (Java)
문제 링크는 여기이고 풀이에 대해서 정리를 해보겠습니다.

문제를 보았을 때, 집의 좌표가 10억까지 가능한 것을 볼 수 있습니다. 굉장히 큰 값이라 그냥 탐색으로는 안될 거 같고 이진탐색으로 해결을 해야 할 것 같습니다.
1. 입력 받기
처음에 입력은 정렬된 순서로 주지 않기 때문에 정렬을 해서 위와 같이 만들었습니다. 그리고 우리가 구해야할 것은 공유기를 설치할 수 있는 집 사이의 최대 거리이기 때문에 이진탐색으로 조건을 걸어서 탐색을 해보겠습니다.
- 집 사이의 최대거리는 9 - 1 = 8 입니다.
- 집 사이의 최소거리는 2 - 1 = 1 입니다.
위의 경우라면 집마다 거리가 1 ~ 8 사이일 것이고, 각 거리들 마다 문제에서 준 공유기의 개수만큼 설치할 수 있는지 여부를 판단해야 합니다.
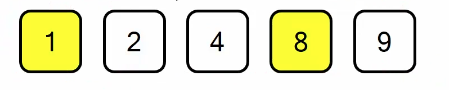
그러면 최대 Gap = 8, 최소 Gap = 1, 중간 Gap = 4로 정의할 수 있습니다. 즉, 집마다 거리를 4이상으로 놓고 공유기를 설치하면 위와 같이 설치할 수 있습니다. 하지만 입력 예시에서는 공유기 개수를 3으로 줬기 때문에 위의 경우는 불가능합니다. 중간 값이 4로 설치 가능한 공유기의 개수가 C보다 작으므로, Gap의 값을 감소시키면 됩니다.
그래서 이번에는 최대 Gap = 3, 최소 Gap = 1, 중간 Gap = 2로 설정하겠습니다.

그리고 집 마다 공유기 설치 거리를 2이상으로 놓고 설치를 해보니 3개를 설치할 수 있습니다. 즉, C(공유기 설치 개수)와 같기 때문에 가능합니다. 하지만 우리는 공유기를 설치할 수 있는 최대 거리를 찾아야 하기 때문에 일단 거리 2를 저장해놓고 더 큰 거리에서 가능한지 확인해보겠습니다.
이번에는 최소 거리를 3, 최대 거리 3, 중간거리 3으로 집마다 거리를 3이상으로 놓고 공유기 설치를 해보겠습니다.

거리를 3이상으로 놓아도 위와 같이 공유기를 C개 이상으로 설치할 수 있습니다. 즉, 거리가 2보다는 3일 때 최대이기 때문에 답은 3이 됩니다.
구현 코드(Java)
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int N = input.nextInt(); // 집의 개수
int C = input.nextInt(); // 공유기의 개수
int[] homeList = new int[N + 1];
for (int i = 1; i <= N; ++i) {
homeList[i] = input.nextInt();
}
Arrays.sort(homeList); // 정렬
int maxResult = 0;
int left = 1;
int right = homeList[N] - homeList[1];
int d = 0;
int ans = 0;
while (left <= right) {
int mid = (left + right) / 2;
int start = homeList[1];
int count = 1; // 공유기 설치 GAP 저장
for (int i = 1; i <= N; ++i) {
d = homeList[i] - start; // 집마다 거리 체크
if (d >= mid) { // 공유기 설치 가능한지 여부 체크
count++;
start = homeList[i]; // 설치 했다면 여기 집 부터 다시 거리 체크
}
}
if (count >= C) {
ans = mid;
left = mid + 1; // 더 많은 Gap에서 공유기 설치할 수 있는지 여부 확인
} else {
right = mid - 1; // 더 적은 Gap에서 공유기 설치할 수 있는지 여부 확인
}
}
System.out.println(ans);
}
}