-
그래프(Graph) 란?Computer Science/Data_Structure 2020. 1. 3. 21:49728x90반응형
그래프의 소개
- 그래프(graph)는 객체 사이의 연결 관계를 표현할 수 있는 자료 구조다. (대표적인 예 : 지도)
- 지도를 그래프로 표현하면 지하철의 특정한 역에서 다른 역으로 가는 최단 경로를 쉽게 찾을 수 있다.
- 운영 체제에서는 프로세스와 자원들이 어떻게 연관되는지를 그래프로 분석하여 시스템의 효율이나 교착상태 유무 등을 알아낼 수 있다.
그래프로 표현할 수 있는 것들
-
도로
-
미로
-
선수과목
1. 그래프의 정의와 용어
그래프의 정의
그래프는 정점(vertex)와 간선(edge)들의 유한 집합이라 할 수 있다. 수학적으로는 G = (V,E)와 같이 표시한다.
V(G)는 그래프의 G의 정점들의 집합, E(G)는 그래프 G의 간선들의 집합이다.
- 정점 : 여러 가지 특성을 가질 수 있는 객체
- 간선 : 이러한 정점들 간의 관계
정점(vertex)는 노드(node)라고도 불리며, 간선(edge)는 링크(link)라고도 불림
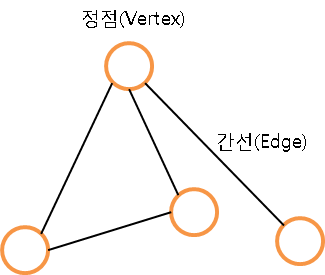
위와 같은 경우처럼 정점(vertex)이 있고 이를 연결하는 간선이 존재한다.
무방향 그래프와 방향 그래프

간선의 종류에 따라 2가지로 구분이 된다
-
무방향 그래프(undirected graph)
- 간선은 간선을 통해서 양방향으로 갈수 있음을 나타낸다. 위의 경우 (A,B) = (B,A) 이다.
-
방향 그래프(directed graph)
- 간선에 방향성이 존재하는 그래프로서 도로의 일반통행길처럼 간선을 통하여 한쪽 방향으로만 갈 수 있음
네트워크
간선에 가중치를 할당하게 되면, 간선의 역할이 두 정점간의 연결 유무뿐만 아니라 연결 강도까지 나타낼 수 있으므로 보다 복잡한 관계를 표현할 수 있게 된다.
이렇게 간선에 비용이나 가중치가 할당된 그래프를
-
가중치 그래프(weighted graph)
-
네트워크(network)
라고 한다.

네트워크는 도시와 도시를 연결하는 도로의 길이 등등 응용 분야가 보다 광범위하다.
부분 그래프
어떤 그래프의 정점의 일부와 간선의 일부로 이루어진 그래프를 부분그래프(subgraph)라 한다.

G2는 G1의 부분그래프 이다.
정점의 차수
그래프에서 인접 정점(adjacent vertex)란 간선에 의해 직접 연결된 정점을 뜻한다.

위의 그래프에서 정점 0의 인접 정점은 정점1, 정점2, 정점3이다.
무방향 그래프에서 정점의 차수(degree)는 그 정점에 인접한 정점의 수를 말한다.
정점0의 차수는 3이다.
무방향 그래프
모든 정점의 차수를 합하면 간선 수의 2배가 된다. 이것은 하나의 간선이 두개의 정점에 인접하기 때문이다. 위의 (a) 그래프에서 모든 정점 차수의 합은 8이고 간선은 5이다.
방향 그래프
- 진입 차수(in-degree) : 외부에서 오는 간선의 개수
- 진출 차수(out-degree) : 외부로 향하는 간선의 개수
경로

위 그림으로 다시 예시를 들어서 설명하려 한다. 위 (a) 그래프에서 0, 2, 3 은 경로지만, 0, 2, 1 은 경로가 아니다. 왜냐하면 정점 2와 정점1을 연결하는 간선이 없기 때문이다.
- 단순 경로 : 경로 중에서 반복되는 간선이 없을 경우에 이러한 경로
- 사이클 : 단순 경로의 시작 정점과 종료 정점이 동일한 이러한 경로
연결 그래프
무방향 그래프 G에 있는 모든 정점쌍에 대하여 항상 경로가 존재한다면 G는 연결되었다고 하며, 이러한 무방향 그래프 G를 연결 그래프(connected graph)라 부른다. 그렇지 않은 그래프는 비연결 그래프(unconnected graph)라 한다. 트리는 그래프의 특수한 형태로서 사이클을 가지지 않는 연결 그래프이다.

G1는 연결 그래프이고, G2는 비연결 그래프 이다.
완전 그래프
그래프에 속해있는 모든 정점이 서로 연결되어 있는 그래프를 완전 그래프(complete graph)라고 한다.

무방향 그래프의 정점 수를 N이라 하면, 하나의 정점은 N-1개의 다른 정점으로 연결되므로 간선의 수는 N(N-1)/2가 된다. 예를들어 완전 그래프에서 N=4라면 간선의 수는 6이다.
그리고 JAVA를 이용해서 그래프를 구현해보고 이 글을 마치려고 한다.
12345678910111213141516171819202122232425262728293031323334353637public class AdjMatrix {int matrix[][];int vertexSize;public AdjMatrix(){matrix = new int[50][50];vertexSize = 0;}public void insertVertex(int v){if(v >= 50){System.out.println("정점의 개수를 초과했습니다");}else{vertexSize++;}}public void insertEdge(int v1, int v2){if(v1 >= vertexSize || v2 >= vertexSize){System.out.println("값이 올바르지 않습니다");}else{matrix[v1][v2] = 1;}}public void printAdjMatrix(){for(int i=0; i<vertexSize; i++){for(int j=0; j<vertexSize; j++){System.out.print(matrix[i][j] + " ");}System.out.println();}}}12345678910111213141516171819202122public class Test {public static void main(String[] args){AdjMatrix m = new AdjMatrix();for(int i=0;i<4;i++){m.insertVertex(i);}m.insertEdge(0,3);m.insertEdge(0,1);m.insertEdge(1,3);m.insertEdge(1,2);m.insertEdge(1,0);m.insertEdge(2,3);m.insertEdge(2,1);m.insertEdge(3,2);m.insertEdge(3,1);m.insertEdge(3,0);m.printAdjMatrix();}}
결과창 Matrix를 이용해서 그래프를 구현하였다.
반응형'Computer Science > Data_Structure' 카테고리의 다른 글
너비 우선 탐색(BFS) 란? (0) 2020.01.04 깊이 우선 탐색(DFS) 란? (0) 2020.01.04 힙(heap) 이란 ? (0) 2020.01.03 이진 탐색 트리(binary search tree) 란? (0) 2020.01.02 이진 트리의 순회 (0) 2020.01.02 - 그래프(graph)는 객체 사이의 연결 관계를 표현할 수 있는 자료 구조다. (대표적인 예 : 지도)