동적 계획법 (Dynamic Programming)이란?

1. 정의

• 동적계획법 (DP 라고 많이 부름)
  • 입력 크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서, 보다 큰 크기의 부분 문제를 해결, 최종적으로 전체 문제를 해결하는 알고리즘
  • Memoization 기법을 사용함
    • Memoization (메모이제이션) 이란: 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않도록 하여 전체 실행 속도를 빠르게 하는 기술
  • 문제를 잘게 쪼갤 때, 부분 문제는 중복되어, 재활용됨
    • 예: 피보나치 수열

 

• 분할 정복
  • 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
    
    • 일반적으로 재귀함수로 구현
  • 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음
    • 예: 병합 정렬, 퀵 정렬 등

 

동적 계획법의 핵심은 하나의 문제를 단 한번만 푸는 것이 핵심이다. 

일반적으로 분할 정복 기법은 동일한 문제를 여러번 풀어 중복이 된다는 단점을 가지고 있다. 하지만 퀵정렬, 병합정렬과 같은 정렬 알고리즘에서는 분할정복 알고리즘에서는 단점이 존재하지 않아 아주 빠른 정렬을 수행할 수 있다.

하지만 '피보나치 수열' 에서 분할정복을 사용한다면 아주 비효율적이 된다. (피보나치 수열은 모두 다 알 것이다)

 

피보나치의 점화식 

 

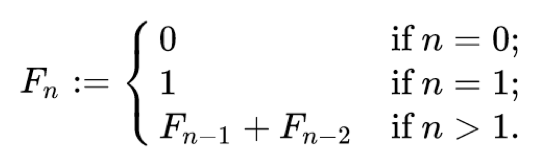
출처 : Fastcampus Algorithms Lecture

 

피보나치 수열은 하나의 수를 구하기 위해서는 구하고 싶은 수 앞에 2개의 수를 알아야 한다.

 

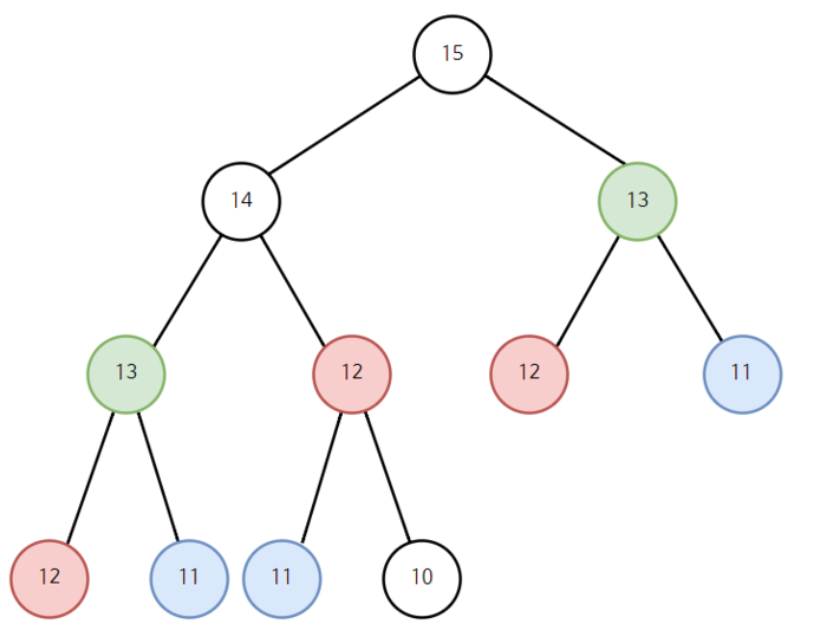
출처 : https://m.blog.naver.com/ndb796/221233570962

 

위와 같이 피보나치 수열에서 분할정복 알고리즘을 사용한다면 12는 3번, 11번 3번이 중복된다.(한번 구한 값을 저장해놓는다면 다시 구할 필요가 없지만, 저장해놓지 않기 때문에 다시 구하는 치명적인 단점이 있다)

 

동적계획법의 가정 2가지

1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 적용이 된다. 

 

2번의 가정이 중요하다. 동적계획법을 다시 말하자면 크고 어려운 문제가 있으면 그것을 작게 나누어 해결한 뒤에 나중에 전체의 답을 구하는 것이다. 이렇게 보면 분할정복과 크게 다른 것이 없어 보이지만, 위에서 설명한 것 처럼 분할정복과의 가장 큰 차이는 동적계획법은 "메모이제이션" 을 사용한다는 것이다. 메모이제이션은 이미 계산한 결과를 배열에 저장해서 다시 그 값이 필요하다면 다시 계산하지 않고 쓰게 위한 역할이다. 

 

 

코드 예제

import java.util.Scanner;
 
public class fibonacci {
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        int n = input.nextInt();
 
        System.out.println(fibo(n));
    }
 
    public static int fibo(int n) {
        if (n <= 1) {
            return n;
        }
 
        return (fibo(n-1 ) + fibo(n-2));
    }
}
 
 

위에는 "메모이제이션" 을 사용하지 않고 재귀 호출만을 사용해서 피보나치 수열을 구현했다. 

이렇게 되면 계속 하나의 값을 구하기 위해서 2개씩 나뉘어 진다(위의 그림처럼 이진 트리 처럼 계속 나뉘어 진다) 따라서 시간복잡도가 2^n이 되므로 n이 조금만 커져도 구할 수가 없게 된다.

 

하지만 여기에서 동적 계획법(Dynamic Programming)을 사용해보자. 

 

public class fibonacci {
    public static int[] fibo_memo;
    
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        int n = input.nextInt();
 
        fibo_memo = new int[100];   // 대략 크기를 100으로 지정
 
        System.out.println(fibo(n));
    }
 
    public static int fibo(int n) {
        if (n <= 1) {
            return n;
        }
 
        if (fibo_memo[n] != 0) { //저장된 값을 다시 필요로 하면 그 값 return
            return fibo_memo[n];
        }
 
        return fibo_memo[n] = fibo(n-1 ) + fibo(n-2);
    }
}
 
 

 

일단 계산한 값을 저장 할 전역 변수 배열을 하나 만들었다. 그리고 계산한 값을 배열에 저장을 해놓는다. 그리고 나중에 다시 계산한 값이 필요하다면 배열 안에 그 값을 return 해주기 때문에 시간이 많이 단축된다.

 

예를 들어서 위의 피보나치 수열 그림을 봐보자. 오른쪽 서브트리에서 13을 이미 계산 했다고 가정하자. 그러면 왼쪽 서브 트리에서 13을 요구할 때 다시 구하려고 재귀함수를 사용하지 않아도 바로 배열안에 저장한 값을 가져오면 되기 때문에 시간이 단축된다. 시간복잡도가 n 까지 줄어든다. 

 

 

 

 

[내용 출처]

https://m.blog.naver.com/ndb796/221233570962

20. 다이나믹 프로그래밍(Dynamic Programming)

자세한 내용은 "동빈나"님 블로그가서 보세요! 유투브도 있으니 이해 잘됩니다.