Dijkstra의 최단 경로 알고리즘이란?

최단 경로 문제 종류

1. 단일 출발 및 단일 도착 (single-source and single-destination shortest path problem) 최단 경로 문제
   • 그래프 내의 특정 노드 u 에서 출발, 또다른 특정 노드 v 에 도착하는 가장 짧은 경로를 찾는 문제
2. 단일 출발 (single-source shortest path problem) 최단 경로 문제
   • 그래프 내의 특정 노드 u 와 그래프 내 다른 모든 노드 각각의 가장 짧은 경로를 찾는 문제

     예를 들면 A, B, C, D 라는 노드를 가진 그래프에서 특정 노드를 A 라고 한다면, A 외 모든 노드인 B, C, D 각 노드와 A 간에 (즉, A - B, A - C, A - D) 각각 가장 짧은 경로를 찾는 문제를 의미함

 

 

2. 최단 경로 알고리즘 - 다익스트라 알고리즘

• 다익스트라 알고리즘은 위의 최단 경로 문제 종류 중, 2번에 해당
  • 하나의 정점에서 다른 모든 정점 간의 각각 가장 짧은 거리를 구하는 문제

 

다익스트라 알고리즘 로직

• 첫 정점을 기준으로 연결되어 있는 정점들을 추가해 가며, 최단 거리를 갱신하는 기법

• 다익스트라 알고리즘은 너비우선탐색(BFS)와 유사

  • 첫 정점부터 각 노드간의 거리를 저장하는 배열을 만든 후, 첫 정점의 인접 노드 간의 거리부터 먼저 계산하면서, 첫 정점부터 해당 노드간의 가장 짧은 거리를 해당 배열에 업데이트

  • 다익스트라 알고리즘의 다양한 변형 로직이 있지만, 가장 개선된 우선순위 큐를 이용한다.

• 우선순위 큐를 활용한 다익스트라 알고리즘

  • 우선순위 큐는 MinHeap 방식을 활용해서, 출발 노드와 가장 짧은 거리를 가진 노드 정보를 먼저 꺼내게 됨

  1) 첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장

  • 초기에는 첫 정점의 거리는 0, 나머지는 무한대로 저장함 (컴퓨터에서 무한대는 없기 때문에 inf 라고 표현함) 
  • 우선순위 큐에 (시작 정점, 거리 0) 만 먼저 넣음 (예를들어서 A가 출발 정점이라고 하면 A에서 A로 가는 거리는 0이기 때문에 0을 출발정점을 넣으라는 뜻이다)

  2) 우선순위 큐에서 노드를 꺼냄

  • 처음에는 첫 정점만 저장되어 있으므로, 첫 정점이 꺼내짐
  • 첫 정점에 인접한 노드들 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교한다. (예를 들어서 배열 안에 0 2 8 6 4 가 들어있다고 가정해보자. 그러면 A에서 B로 가는 거리 = 2, A에서 C로 가는 거리 8 이런식으로 각각 저장이 되어 있는 것이다)  
  • 배열에 저장되어 있는 거리보다, 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트한다. 
  • 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 넣는다.
    • 결과적으로 너비 우선 탐색 방식과 유사하게, 첫 정점에 인접한 노드들을 순차적으로 방문하게 됨
    • 만약 배열에 기록된 현재까지 발견된 가장 짧은 거리보다, 더 긴 거리(루트)를 가진 (노드, 거리)의 경우에는 해당 노드와 인접한 노드간의 거리 계산을 하지 않음

  3) 2번의 과정을 우선순위 큐에 꺼낼 노드가 없을 때까지 반복한다.

 

3. 다익스트라 알고리즘 (우선순위 큐 활용)

 

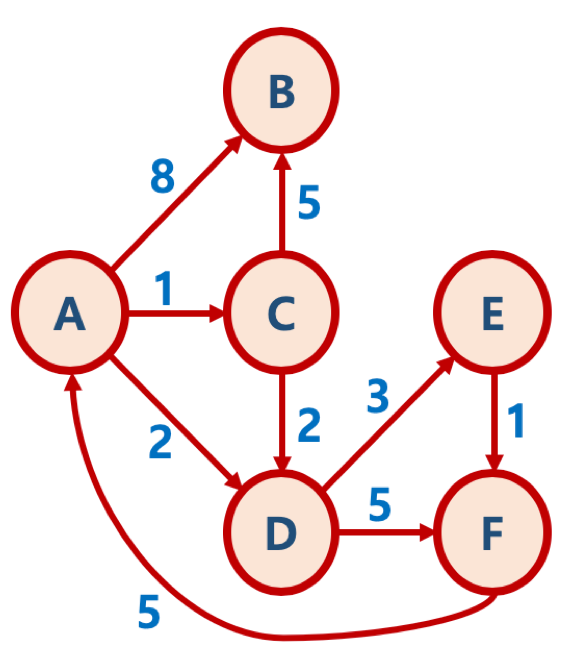
출처 : FastCampus's Algorithms lecture

 

들어가기 전

(A, 0), (C, 1) 이렇게 쓰는 의미는 출발 정점이 A이므로 A에서 C로 가는거리가 1이라는 뜻이다. (D, 2)도 A에서 D로 가는 거리가 2라는 뜻이므로 생각하면서 아래 내용을 이해해보자.

 

1단계: 초기화

• 시작 정점을 기준으로 배열을 선언하여 시작 정점에서 각 정점까지의 거리를 저장
  • 초기에는 시작 정점의 거리는 0, 나머지는 무한대로 저장함 (inf 라고 표현함)
  • 우선순위 큐에 (첫 정점, 거리 0) 만 먼저 넣음 (시작 정점에서 시작 정점으로 가는 거리는 0이기 때문)

 

출처 : FastCampus's Algorithms lecture

위와 같이 출발 정점을 A로 정하였고, A에서 A로 가는 거리는 0이기 때문에 배열안에 0으로 만들고, 우선순위 큐에 A를 넣는다. 그리고 배열의 의미는 다시 말하자면 A에서 A를 가는거리, A에서 B를 가는거리, A에서 C를 가는거리 이렇게 구성되어 있다고 생각하면 된다. 그러나 지금은 배열 처음을 제외하고 나머지는 inf가 들어있는 것을 알 수 있다.

 

 

 

 

2단계: 우선순위 큐에서 추출한 (A, 0) 

• 우선순위 큐에서 노드를 꺼냄
  • 처음에는 첫 정점만 저장되어 있으므로, 첫 정점이 꺼내짐
  • 첫 정점에 인접한 노드들 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교한다.
  • 배열에 저장되어 있는 거리보다, 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트한다.
  • 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 넣는다.

 

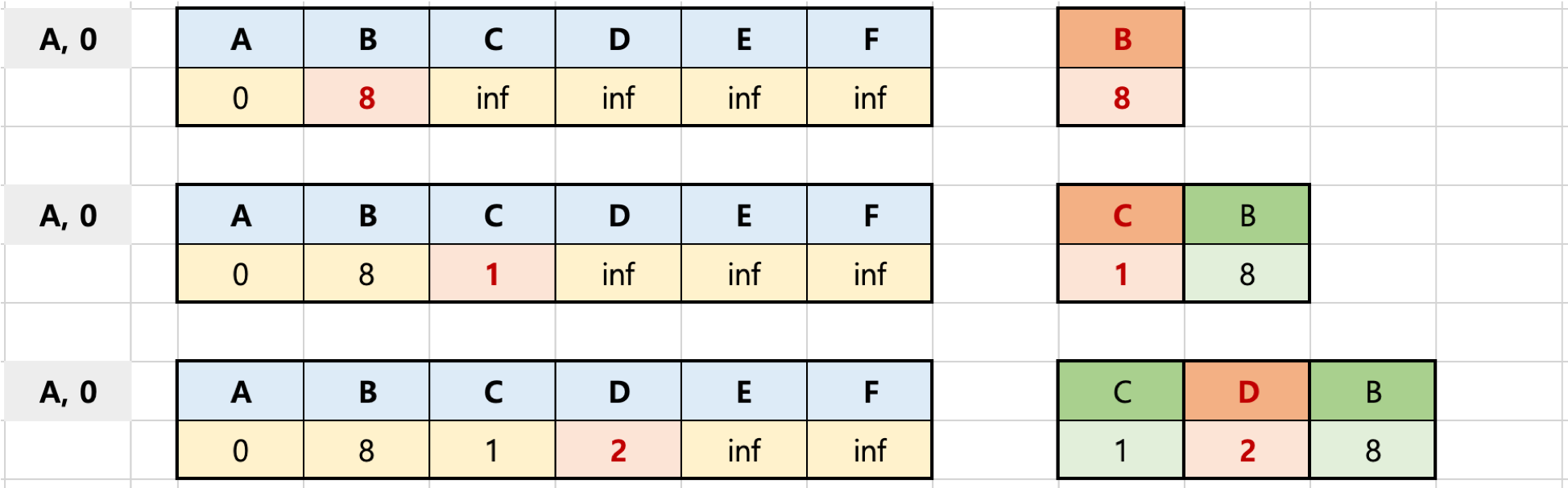
출처 : FastCampus's Algorithms lecture

그 다음에는 A와 인접한 노드 B, C, D를 우선순위 큐에 넣는다. A에서 B로의 거리는 8이고, A에서 C로의 거리는 1, A에서 D의 거리는 2이다. 이것은 inf 보다는 작은 값이므로 배열안의 값들을 업데이트 한다. 

 

 

3단계: 우선순위 큐에서 거리가 가장 짧은 (C, 1) 

• 우선순위 큐가 MinHeap(최소 힙) 방식이므로, 위 표에서 넣어진 (C, 1), (D, 2), (B, 8) 중 (C, 1) 이 먼저 추출됨 (pop)
• 위 표에서 보듯이 1단계까지의 A - B 최단 거리는 8 인 상황임
  • A - C 까지의 거리는 1이다. C 에 인접한 B, D 노드에서 C - B는 5이고, 즉 A - C - B 거리는 1 + 5 = 6 이므로, A - B 최단 거리 8보다 더 짧기 때문에, 이를 배열에 업데이트 한다.
    • 배열에 업데이트했으므로 노드B 거리 6 (즉 A에서 B까지의 현재까지 발견한 최단 거리) 값이 우선순위 큐에 넣어짐
  • C - D 의 거리는 2, 즉 A - C - D 는 1 + 2 = 3 이므로, A - D의 현재 최단 거리인 2 보다 긴 거리, 그래서 D 의 거리는 업데이트되지 않음

 

출처 : FastCampus's Algorithms lecture

 

4단계: 우선순위 큐에서 (C,1)다음으로 거리가 짧은 (D, 2) 

• 지금까지 A노드에서 접근하지 못했던 E와 F 거리가 계산됨
  • A - D 까지의 거리인 2 에 D - E 가 3 이므로 이를 더해서 (E, 5)
  • A - D 까지의 거리인 2 에 D - F 가 5 이므로 이를 더해서 (F, 7)

 

출처 : FastCampus's Algorithms lecture

따라서 배열안에 E와 F가 5와 7로 업데이트가 된 후에 우선순위 큐에 들어간 것을 알 수 있다. 

 

 

5단계: 우선순위 큐에서 (E, 5) 

• A - E 거리가 5인 상태에서, E에 인접한 F를 가는 거리는 1이다. 즉 A - E - F 는 5 + 1 = 6, 현재 배열에 A - F 최단거리가 7로 기록되어 있으므로, (F, 6) 으로 업데이트
  • 우선순위 큐에 F, 6 추가(거리 6이 7보다 짧기 때문에 업데이트 됨)

 

출처 : FastCampus's Algorithms lecture

 

 

6단계: 우선순위 큐에서 (B, 6), (F, 6) 를 순차적으로 추출

• 위의 방향 그래프에서 B 노드는 다른 노드로 가는 루트가 없음
• F 노드는 A 노드로 가는 루트가 있으나, 현재 A - A 가 0 인 반면에 A - F - A 는 6 + 5 = 11, 즉 더 긴 거리이므로 업데이트되지 않음

 

출처 : FastCampus's Algorithms lecture

 

7단계: 우선순위 큐에서 (F, 7), (B, 8) 를 순차적으로 추출

• A - F 로 가는 하나의 루트의 거리가 7 인 상황이나, 배열에서 이미 A - F 로 가는 현재의 최단 거리가 6인 루트의 값이 있는 상황이므로, 더 긴거리인 F, 7 루트 기반 인접 노드까지의 거리는 계산할 필요가 없음
  • 계산하더라도 A - F 거리가 6인 루트보다 무조건 더 긴거리가 나올 수 밖에 없음
• B, 8 도 현재 A - B 거리가 6이므로, 인접 노드 거리 계산이 필요 없음.

우선순위 큐를 사용하면 불필요한 계산 과정을 줄일 수 있음

 

 

출처 : FastCampus's Algorithms lecture

 

우선순위 큐 사용 장점

• 지금까지 발견된 가장 짧은 거리의 노드에 대해서 먼저 계산
• 더 긴 거리로 계산된 루트에 대해서는 계산을 스킵할 수 있음

 

 

 

Dijkstra 알고리즘 코드 구현 with Java

import java.util.PriorityQueue;
 
class Element implements Comparable<Element> {
    int index;
    int distance;
 
    public Element(int index, int distance) {
        this.index = index;
        this.distance = distance;
    }
 
    @Override
    public int compareTo(Element o) {
        return this.distance - o.distance;
    }
}
 
public class DijkstraTest {
    static boolean[] visited;
    static int[] dist;
    static int[][] ad;
    static int E = 9, V = 6;
    static int inf = 100000;
 
    public static void DijkstaMethod(int start) {
        PriorityQueue<Element> pq = new PriorityQueue<>();
        dist[start] = 0;
        pq.offer(new Element(start, dist[start]));
 
        while(!pq.isEmpty()) {
            int cost = pq.peek().distance;
            int here = pq.peek().index;
            pq.poll();
 
            if (cost > dist[here]) {   // 현재 배열에 있는 값(최단 거리)보다 cost(거리)가 더 길면 continue
                continue;
            }
 
            System.out.print(here + " ");
 
            // 아래 for문이 다익스트라의 핵심 코드라고 생각함
            for (int i = 1; i <= V; ++i) {   // 업데이트 시켜주는 for문
                if (ad[here][i] != 0 && dist[i] > (dist[here] + ad[here][i])) {
                    // if 문 조건을 잘 생각하기 (업테이트를 위함)
                    dist[i] = dist[here] + ad[here][i];
                    pq.offer(new Element(i, dist[i]));
                }
            }
 
            System.out.println();
 
            for (int i = 1; i <= V; ++i) {   // dist 배열의 중간 결과 보여주기
                System.out.print(dist[i] + " ");
            }
        }
 
    }
 
    public static void main(String[] args) {
        visited = new boolean[V + 1];
        dist = new int[V + 1];
        ad = new int[V + 1][V + 1];
 
        for (int i = 1; i <= V; ++i) {
            dist[i] = inf;
        }
 
        ad[1][2] = 8;
        ad[1][3] = 1;
        ad[1][4] = 2;
        ad[3][4] = 2;
        ad[3][2] = 5;
        ad[4][5] = 3;
        ad[4][6] = 5;
        ad[5][6] = 1;
        ad[6][1] = 5;
 
        DijkstaMethod(1);
 
    }
}
 

 

 

 

 

[출처] - 패스트 캠퍼스 강의자료에서 가져온 내용입니다. 자세한 내용은 강의를 참고해주세요. 

https://www.fastcampus.co.kr/dev_online_algo/

[올인원 패키지] 알고리즘/기술면접 완전 정복 Online | 패스트캠퍼스