Prim 알고리즘 이란?

1. 프림 알고리즘 (Prim's algorithm)

• 대표적인 최소 신장 트리 알고리즘
  • Kruskal’s algorithm (크루스칼 알고리즘), Prim's algorithm (프림 알고리즘)
• 프림 알고리즘
  • 시작 정점을 선택한 후, 정점에 인접한 간선 중 최소 간선으로 연결된 정점을 선택하고, 해당 정점에서 다시 최소 간선으로 연결된 정점을 선택하는 방식으로 최소 신장 트리를 확장해가는 방식
• Kruskal's algorithm 과 Prim's algorithm 비교
  • 둘다, 탐욕 알고리즘을 기초로 하고 있음 (당장 눈 앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾음)
  • Kruskal's algorithm은 가장 가중치가 작은 간선부터 선택하면서 MST를 구함
  • Prim's algorithm은 특정 정점에서 시작, 해당 정점에 연결된 가장 가중치가 작은 간선을 선택, 간선으로 연결된 정점들에 연결된 간선 중에서 가장 가중치가 작은 간선을 택하는 방식으로 MST를 구함

 

 

2. 그림으로 이해하는 프림 알고리즘

1. 임의의 정점을 선택, '연결된 노드 집합'에 삽입
2. 선택된 정점에 연결된 간선들을 간선 리스트에 삽입
3. 간선 리스트에서 최소 가중치를 가지는 간선부터 추출해서,
   1. 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 이미 들어 있다면, 스킵함(cycle 발생을 막기 위함)
   2. 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 들어 있지 않으면, 해당 간선을 선택하고, 해당 간선 정보를 '최소 신장 트리'에 삽입
4. 추출한 간선은 간선 리스트에서 제거
5. 간선 리스트에 더 이상의 간선이 없을 때까지 3-4번을 반복

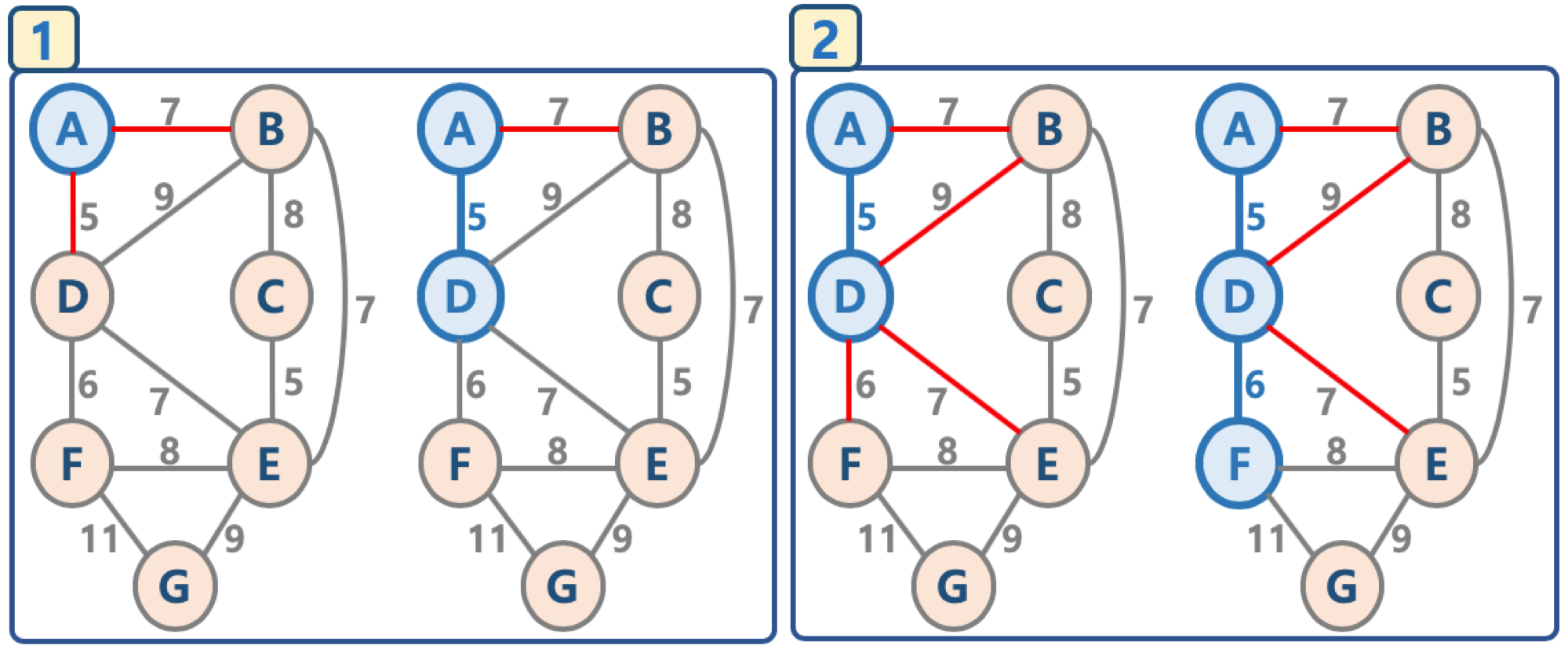
출처 : fastcampus's Algorithms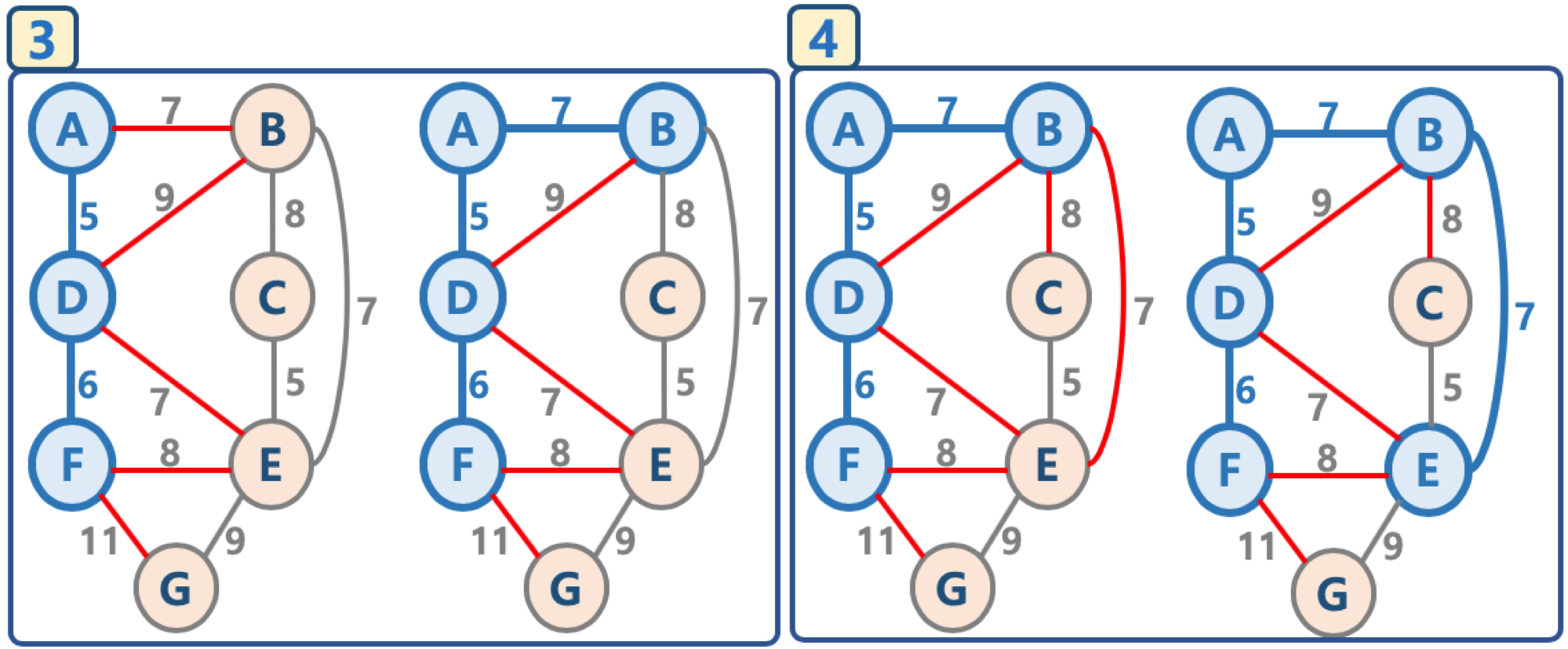 

출처 : fastcampus's Algorithms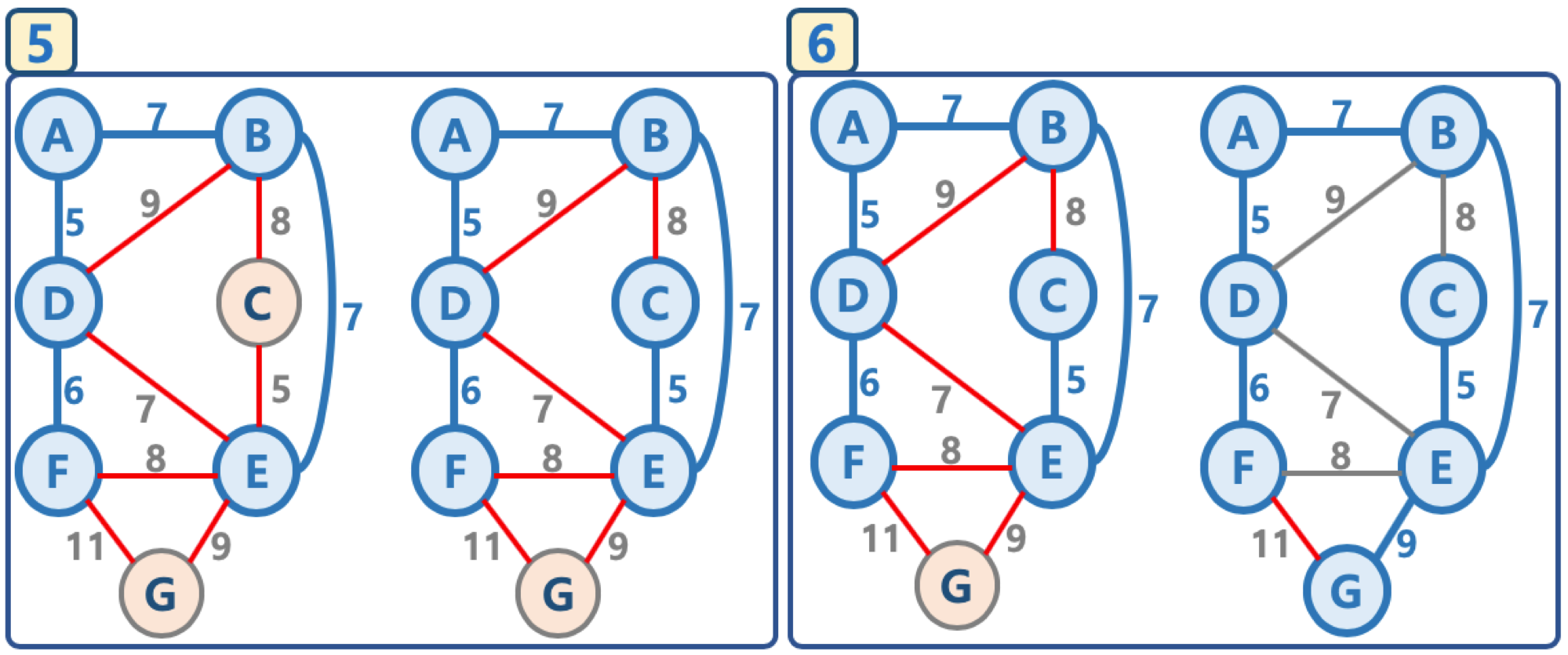

출처 : fastcampus's Algorithms

위의 그림은 설명 순서대로 반복하면 Prim's Algorithms으로 MST를 만들 수 있다. 그런데 하나만 설명하려 한다. 

• 해당 간선에 연결된 인접 정점이 '연결된 노드 집합'에 이미 들어 있다면, 스킵함(cycle 발생을 막기 위함)

이 말이 조금 이해가 안될 수도 있다. 예를들어 그림 4번을 보자. B와 E의 간선 가중치 7을 선택한 후에 그 다음에 작은 간선 가중치인 DE가 존재한다. 하지만 DE는 양쪽 노드 '연결된 노드 집합'에 들어 있기 때문에 포함시키지 않는다는 뜻이다.  

 

 

import java.util.*;
 
public class Prim {
    static int V, E, min = 0;
    static Graph graph;
    static boolean[] visited;
    static ArrayList<Edge> mst;
 
    public static void main(String[] args) {
        V = 7;
        E = 9;
        visited = new boolean[V + 1];
        mst = new ArrayList<>();
        graph = new Graph(V);
 
        graph.AddEdge(1, 6, 10);
        graph.AddEdge(1, 2, 29);
        graph.AddEdge(2, 3, 16);
        graph.AddEdge(2, 7, 15);
        graph.AddEdge(3, 4, 12);
        graph.AddEdge(4, 5, 22);
        graph.AddEdge(4, 7, 18);
        graph.AddEdge(5, 7, 25);
        graph.AddEdge(5, 6, 27);
 
        PrimMethod();
 
        for (Edge edge : mst) {
            System.out.println(edge.start + " - " + edge.end + " cost : " + edge.cost);
        }
        System.out.println(min);
    }
 
    public static void PrimMethod() {
        PriorityQueue<Edge> pq = new PriorityQueue<>();  // 가중치가 낮은 순대로 간선은 정렬함
        Queue<Integer> q = new LinkedList<>();           // 정점 방문 스케줄 처리를 위한 큐
        q.add(1);                                        // 시작 정점은 1로 선택
 
        while(!q.isEmpty()) {
            int start = q.poll();
            visited[start] = true;
 
            for (Edge edge : graph.edge[start]) {        // 현재 정점 start와 연결된 간선중
                if (!visited[edge.end]) {                // 아직 정점 end를 방문하지 않았다면
                    pq.add(edge);                        // 우선순위 큐에 간선을 추가한다.
                }
            }
 
            while(!pq.isEmpty()) {
                Edge edge = pq.poll();                  // 가중치가 가장 적은 간선이 나올 것이며
                if (!visited[edge.end]) {               // 간선이 연결된 정점 end를 방문한 적이 없다면
                    q.add(edge.end);                    // 큐에 넣고 다음에 방문한다.
                    visited[edge.end] = true;           // 방문했떤 정점을 다시 방문하지 않도록 표시
                    mst.add(edge);                      // 최소 스패닝 트리를 구성하는 간선 추가
                    System.out.println(edge.cost);
                    min += edge.cost;                   // 가중치 최소 값을 하나씩 더함
                    break;                             // break 하는 이유는 1과 연결된 간선 중 최소 간선만 더하고
                }                                      // 나머지 간선은 더하지 않기 위해서 탈출 하는 것임
            }
        }
 
    }
}
 
class Graph {
    List<Edge>[] edge;
 
    public Graph(int V) {
        edge = new LinkedList[V + 1];
        for (int i = 1; i <= V; ++i) {
            edge[i] = new LinkedList<>();
        }
    }
 
    // 양방향 그래프
    public void AddEdge(int start, int end, int cost) {
        edge[start].add(new Edge(start, end, cost));
        edge[end].add(new Edge(end, start, cost));
    }
}
 
class Edge implements Comparable<Edge> {
    int start, end, cost;
 
    public Edge(int start, int end, int cost) {
        this.start = start;
        this.end = end;
        this.cost = cost;
    }
 
    @Override
    public int compareTo(Edge o) {
        return this.cost - o.cost;
    }
}
 

 

 

 

[Reference]

fastcampus Algorithms lecture