합병 정렬(merge sort) 란?

합병 정렬의 개념

합병 정렬(merge sort)는 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트를 얻고자 하는 것이다. 합병 정렬은 분할 정복(divide and conquer) 기법에 바탕을 두고 있다. 분할 정복 기법은 대게 순환 호출을 이용하여 구현된다. 

 

1. 분할(divide) : 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
2. 정복(Conquer) : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 기법을 적용한다.
3. 결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 통합한다.

 

위의 과정을 그림으로 보면서 이해해보자.

 

 

출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

 

 

다시 말하면, 위와 같이 배열의 크기가 1이 될 때 까지 분할(divide)를 한 후에 거기서 옆에 있는 애와 정복(Conquer)을 한 후에 다시 결합(Combine)하는 과정을 계속 반복한다.

 

 

합병 정렬의 과정

• 실제로 정렬이 이루어지는 시점은 2개의 리스트를 합병(merge)하는 단계이다.
• 합병 정렬은 추가적인 리스트를 필요로 한다.
• 2개의 리스트의 요소들을 처음부터 하나씩 비교하여 두개의 리스트의 요소 중에서 더 작은 요소를 새로운 리스트로 옮긴다.
• 둘 중에서 하나가 끝날 때 까지 이 과정을 되풀이한다.
• 만약 둘 중에서 하나의 리스트가 먼저 끝나게 되면 나머지 리스트의 요소들을 전부 새로운 리스트로 복사한다.

 

 

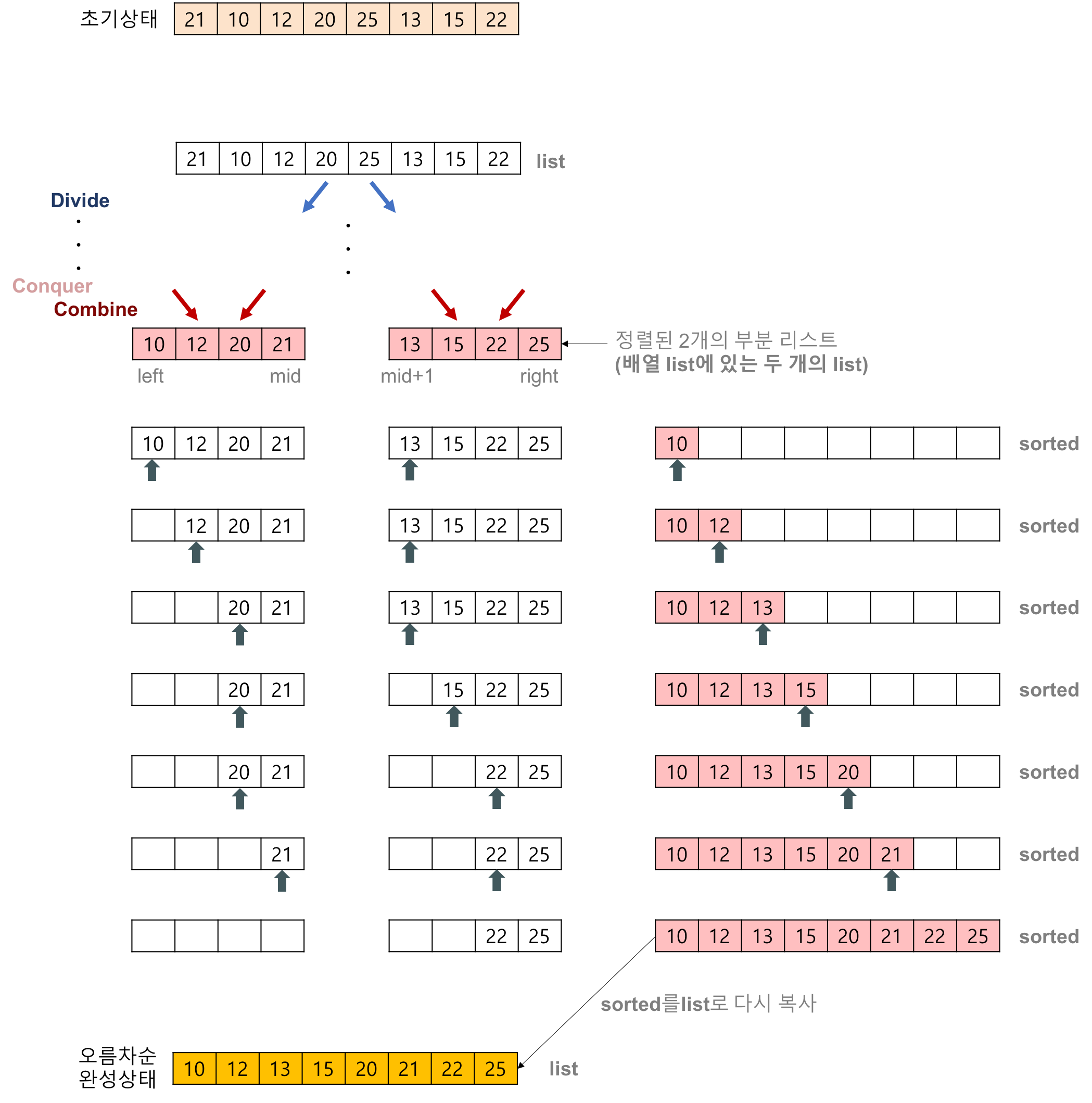
출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

 

처음에 반으로 계속 나눈 후에 정렬을 하면서 돌아 왔을 때 위의 경우에서 2개의 리스트 (크기가 4인 리스트 2개가 있을 때) 를 어떻게 다시 8개로 합칠 수 있는지에 대한 과정을 나타내고 있다. 

 

자바로 합병 정렬을 구현해보자. 

 

public class MergeSort {
    static int[] sorted = new int[8];
 
    public static void merge(int list[], int left, int mid, int right){
        int i = left, j = mid+1, k = left, l; 
 
        while (i <= mid && j <= right) {
            if  (list[i] <= list[j]) {
                sorted[k++] = list[i++];
            } else {
                sorted[k++] = list[j++];
            }
        }
 
        if (i > mid){
            for(l = j; l< = right; l++){
                sorted[k++] = list[l];
            }
        }
        else {
            for(l = i; l <= mid; l++){
                sorted[k++] = list[i];
            }
        }
 
        for (l = left; l <= right; l++){
            list[l] = sorted[l];
        }
    }
 
    public static void merge_sort(int list[], int left, int right){
        int mid;
        if(left < right){
            mid = (left + right ) /2;
            merge_sort(list, left, mid);
           merge_sort(list,mid + 1, right);
           merge(list, left, mid, right);
        }
    }
 
    public static void main(String[] args){
        int[] list = {27, 10, 12, 20, 25, 13, 15, 22};
       merge_sort(list, 0, list.length-1);
 
        for(int q = 0; q < list.length; q++){
            System.out.print(list[q] + " ");
        }
 
    }
}

 

 

 

합병 정렬의 복잡도 분석 

합병 정렬에서 비교 연산과 이동 연산이 몇 번이나 수행되는 지를 생각해보자. 합병 정렬은 순환 호출 구조로 되어 있다.

따라서 배열의 개수 n이 2의 거듭제곱이라고 가정하고 순환 호출의 깊이가 얼마나 되느지는 생각해보자.

 

만약 n이 2의3제곱인 경우에는 부분 배열의 크기가 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 따라서 일반적으로 n = 2^k 라고 하면 배열의 크기는 2^k -> 2^k-1 -> ... 2^0이 되어 순환 호출의 깊이가 k가 될 것임을 알 수 있다. 여기서 k = log2n 임을 알 수 있다. (밑이2 인 로그 이다)

 

 

 

출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

 

그림을 보면 좀 더 이해가 간다. 나눠질 때 반으로 쪼개지니까 나누기 2를 한 것과 같다. 계산하기 쉽게 n 을 2의 거듭제곱이라고 가정을 했으니, 배열의 크기가 1일 때 까지 분할(Divide) 과정을 진행하니 깊이와 2의 거듭제곱의 지수와 같다는 것을 알 수 있다. 

 

 

분할(Divide)

• 배열이 부분 배열로 나누어지는 단계에서는 비교 연산이나 이동 연산이 수행되지 않는다.

합병(Merge)

• 부분 배열이 합쳐지는 merge 함수에서 비교 연산과 이동 연산이 수행된다.

 

순환호출의 깊이만큼의 합병 단계가 필요하다. 

 

 

그러면 각 합병 단계에서 비교연산은 몇번이나 수행 될까?

• n = 2^3일 때 크가 1인 부분 배열 2개를 합병하는 데는 최대 2개의 비교 연산이 필요하다.
• 부분 배열의 쌍이 4개이므로 2*4 = 8번의 비교 연산이 필요하다 
• 다음 단계에서 크기가 2인 부분 배열을 2개 합치는데 최대 4번의 비교 연산이 필요하다.
• 부분 배열 쌍이 2쌍이 있으므로 역시 4*2 = 8번의 연산이 필요하다
• 마지막 합병 단계인 크기가 4인 부분 배열2개를 합병하는 데는 최대 8번의 비교 연산이 필요하다.

일반적인 경우에서는 하나의 합병단계에서는 최대 n번의 비교 연산이 필요함을 알 수 있다. 

따라서 합병 단계(깊이)가 k=log2n(밑이2)번 만큼 있으므로 총 비교 연산은 최대 nlog2n번 필요하다.

 

 

이동 연산은 얼마나 수행되는 것일까? 

• 하나의 합병 단계에서 보면 임시 배열에 복사했다가 다시 가져와야 한다.
• 이동 연산은 총 부분 배열에 들어 있는 요소의 개수가 n인 경우, 레코드의 이동이 2n번 발생한다.
• 따라서 log2n개의 합병 단계가 필요하므로 총 2nlog2n개의 이동 연산이 필요하다. 

 

 

왜 2n번인가에 대해서 생각을 해보니, 일단 임지 배열로 정렬을 한 후에 현재 합병 할 만큼의 수를 옮겨야 한다. 그리고 다시 정렬된 임시배열을 다시 원래 배열에 옮겨야 하므로 2n번이 발생하는 것이다.

 

결론적으로 합병정렬은 비교 연산과 이동 연산의 경우 O(nlog2n)의 복잡도를 가진다.

 

 

합병 정렬의 장단점

• 장점

  • 안정적인 정렬 방법이며 데이터의 분포에 영향을 덜 받는다.
  • 입력 데이터가 무엇이든간에 정렬되는 시간은 동일하다.
  • 즉 최악, 평균, 최선의 경우가 다 같이 O(nlogn)인 정렬 방법이다.

• 단점

  • 임시 배열이 필요하다
  • 배열의 크기가 큰 경우에는 이동 횟수가 많으므로 합병 정렬은 매우 큰 시간적 낭비를 초래한다.
  • 그러나 만약 연결 리스트로 구성하여 합병 정렬할 경우, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다. 
  • 따라서 크기가 큰 레코드를 정렬할 경우, 만약 연결리스트를 사용한다면 합병 정렬은 퀵 정렬을 포함한 다른 어떤 정렬 방법보다 효율적일 수 있다. 

 

 

출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

 

이렇게 병합 정렬의 경우 최악, 평균, 최선의 경우에서 모두 동일하다는 것을 알 수 있으며 구현이 쉽지 않지만 상당히 빠른 정렬 중에 하나이다.