-
퀵 정렬(quick sort)Computer Science/Data_Structure 2020. 1. 8. 22:36728x90반응형
퀵 정렬의 개념
퀵 정렬(quick sort)은 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법이다. 퀵정렬도 분할-정복(divide and conqure)에 근거한다. 퀵 정렬은 합병 정렬과 비슷하게 전체 리스트를 2개의 부분 리스트로 분할하고, 각각의 부분 리스트를 다시 퀵정렬하는 전형적인 분할-정복법을 사용한다.
그러나 합병 정렬과는 달리 퀵 정렬은 리스트를 다음과 같은 방법에 의해 비균등하게 분할한다. 먼저 리스트 안에 있는 한 요소를 피벗(pivot)으로 선택한다.
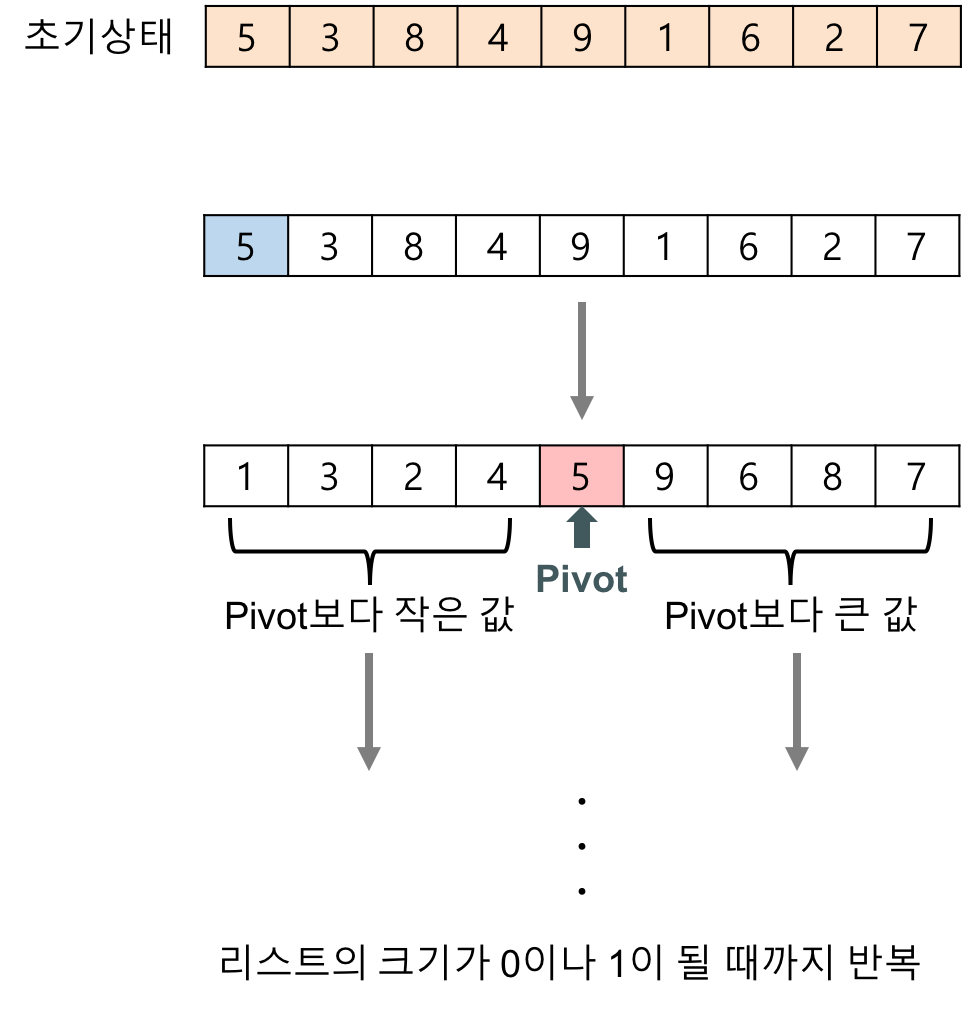
출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html 처음에 리스트의 첫 번째 요소인 5를 피벗(pivot)으로 정하였다.
- 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다.
- 결과적으로 피벗을 중심으로 왼쪽은 피벗보다 작은 요소들로 구성되고, 오른쪽은 피벗보다 큰 요소들로 구성된다.
- 이 상태에서 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬하게 되면 전체 리스트가 정렬된다.
그러면 퀵 정렬은 어떻게 왼쪽 부분 리스트와 오른쪽 부분 리스트를 정렬할까?
- 퀵 정렬은 순환호출을 이용한다.
- 부분 리스트에서도 다시 피봇을 정하고 피봇을 기준으로 2개의 부분 리스트로 나누는 과정이 되풀이 된다.
- 부분 리스트들이 더 이상이 분할이 불가능할 때 까지 나누어진다.
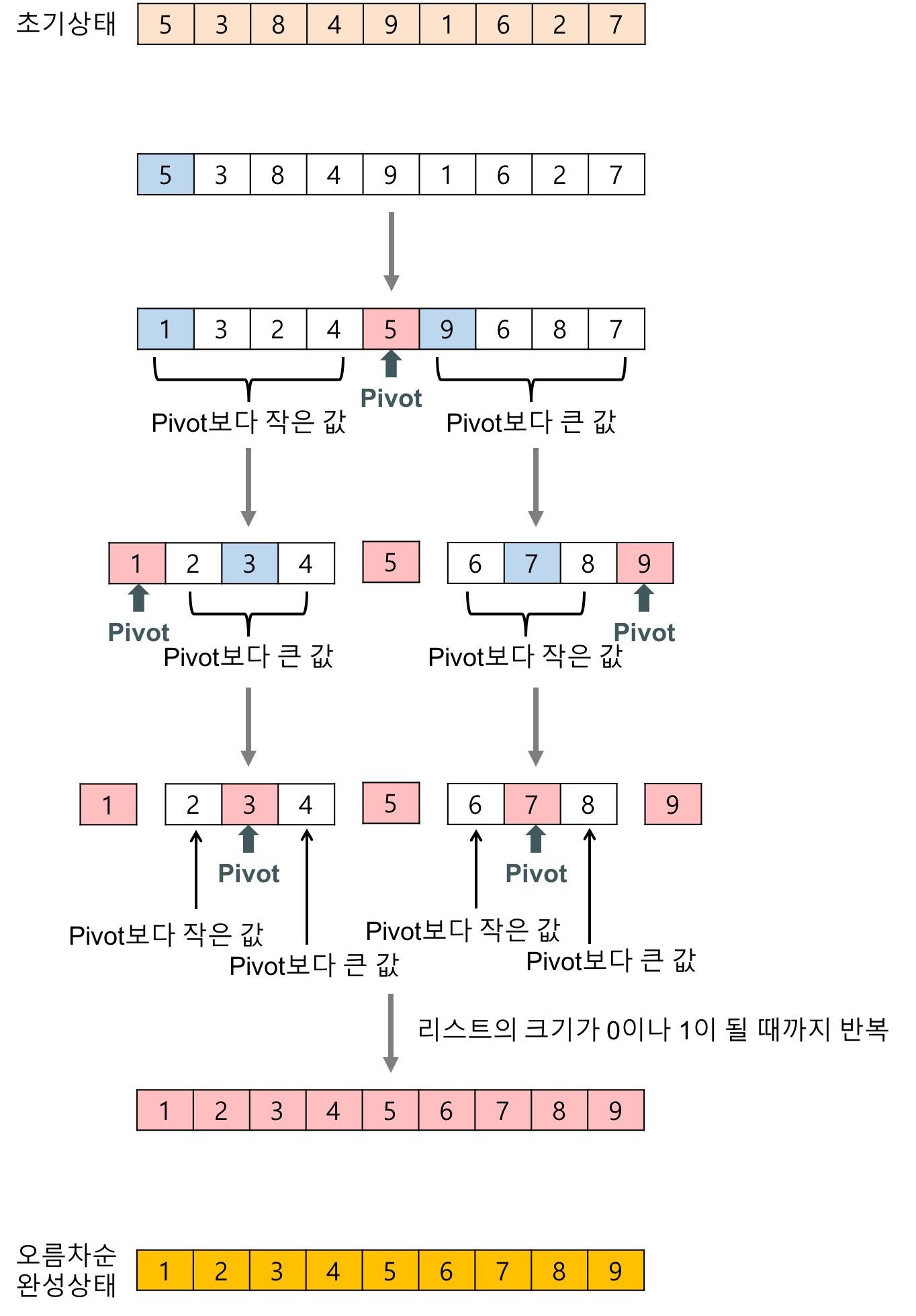
출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html 위의 그림은 간단히 pivot 을 정한 것을 기준으로 리스트를 2개를 나누고 양 쪽 리스트에서 또 pivot을 정한 것을 기준으로 나눠서 계속 진행하는 것을 나타내는 그림이다.
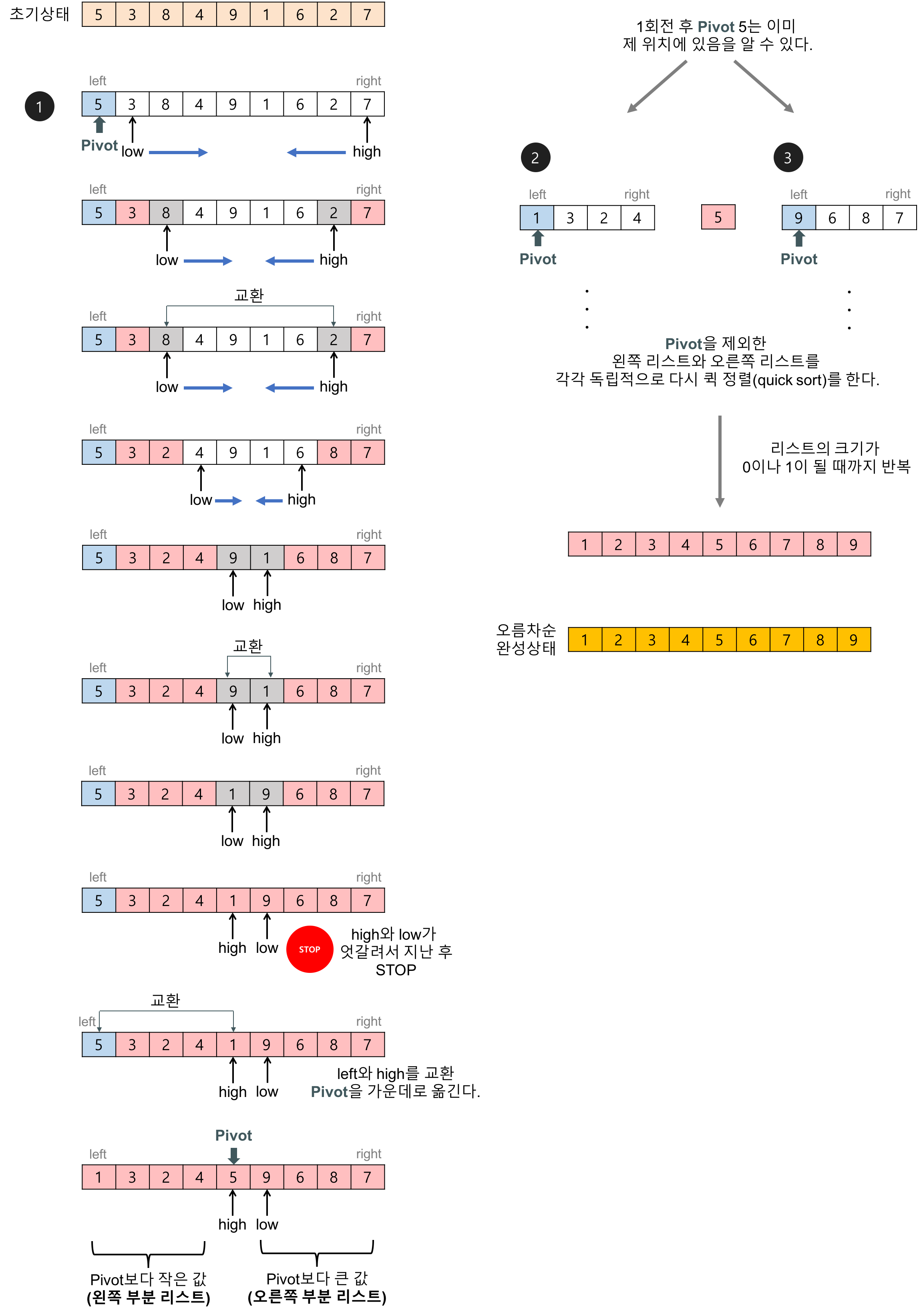
출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html 먼저 간단히 진행 하기 위해서 피봇값을 입력 리스트의 첫번째 데이터로 하자. (따라서 피봇값은 5이다)
2개의 인덱스 변수 low와 high를 이용하자. low는 왼쪽 부분 리스트를 만드는데 사용하고 high는 오른쪽 부분 리스트를 만드는데 사용한다.
- 인덱스 변수 low : 왼쪽에서 오른쪽으로 탐색해가다가 피벗보다 큰 데이터를 찾으면 멈춘다.
- 인덱스 변수 high : 오른쪽 끝에서부터 왼쪽으로 탐색해가다가 피벗보다 작은 데이터를 찾으면 멈춘다.
- low와 high가 서로 엇갈리게 되면 멈춰서 피봇과 high인덱스가 가르키는 것의 자리를 이동시키게 되면 피봇을 기준으로 2개의 리스트로 나누어지게 된다.
- 엇갈린다는 말은 작은 값의 인덱스가 큰 값의 인덱스보다 작은 상황이다.
이제 자바로 퀵 정렬을 구현해보자.
123456789101112131415161718192021222324252627282930313233343536373839404142public class QuickSort {static int partition(int[] list, int left, int right){int pivot;pivot = list[left];while (left < right) {while ((list[left] < pivot) && (left < right))left++;while ((list[right] > pivot) && (left < right))right--;if (left < right) {int temp = list[left];list[left] = list[right];list[right] = temp;}}return left;}static void quick_sort(int[] list, int left, int right){if(left < right){int q = partition(list, left, right);quick_sort(list, left,q - 1);quick_sort(list,q + 1, right);}}public static void main(String[] args){int[] list = {5,3,8,4,9,1,6,2,7};quick_sort(list,0,list.length-1);for(int i=0; i<list.length; i++){System.out.print(list[i] + " ");}}}퀵 정렬의 복잡도 분석
n이 2의 거듭제곱이라고 가정하고 만약에 퀵정렬에서의 리스트 분할이 항상 리스트의 가운데에서 이루어진다고 가정하면 합병 정렬의 복잡도 분석과 마찬가지로 n개의 레코드를 가지는 리스트는 n/2, n/4, n/8 ... n/2^k의 크기로 나누어질 것이다. 크기가 1이 될 때까지 나누어지므로 n/2^k =1일 때까지 나누어질 것이고 따라서 k = log2n 이다.
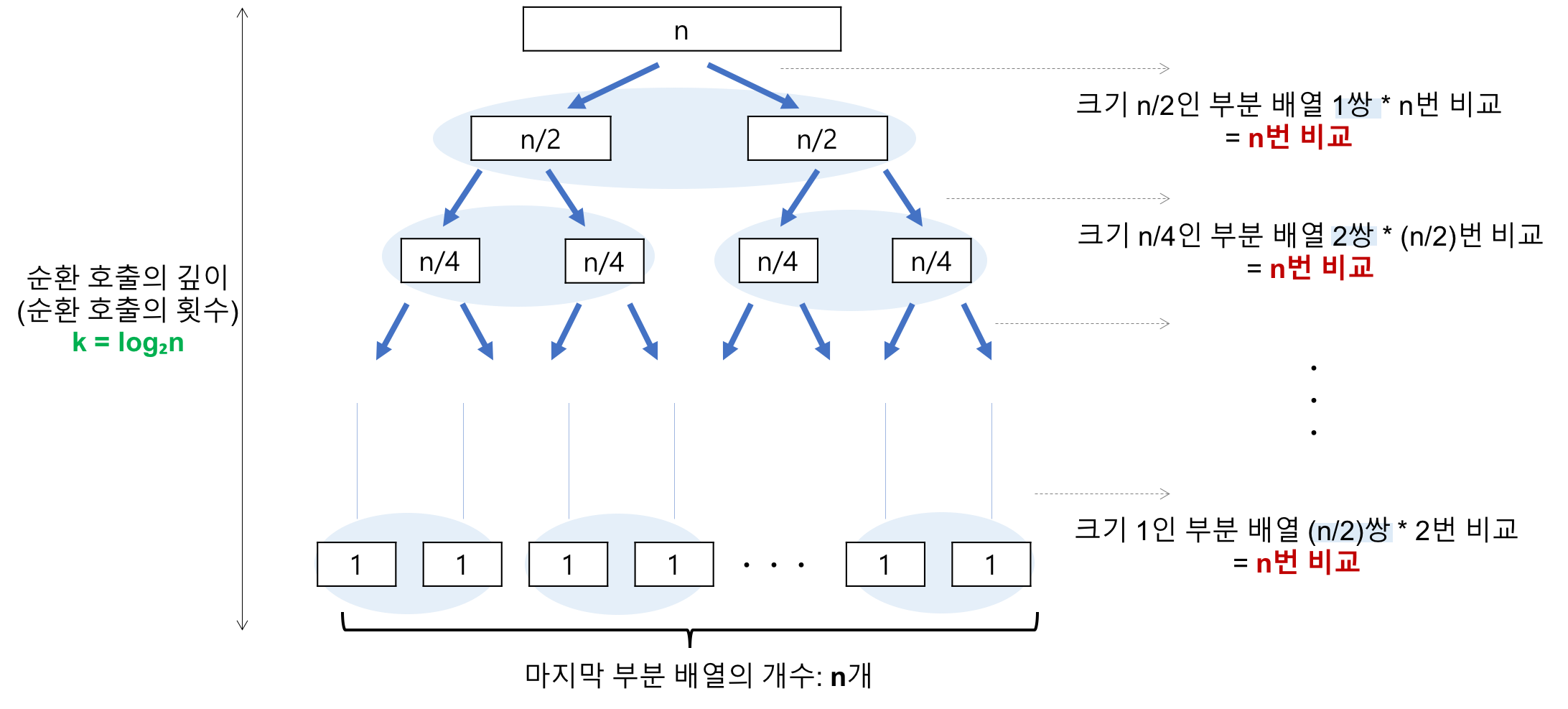
출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html 각각의 높이 위치에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어지므로 퀵정렬은 비교 연산을 총 nlog2n번 실행하게 되어 O(nlog2n)의 복잡도를 가지는 알고리즘이 된다. (높이가 log2n이기 때문)
여기서 레코드의 이동횟수는 비교 횟수보다 적으므로 무시할 수 있다.
퀵 정렬에서의 최악의 경우
리스트가 계속 불균형하게 나누어지는 것이다. 이런 경우, 퀵 정렬의 높이의 개수는 n이 되고, 한번의 패스에서 평균 n번 정도의 비교 연산이 필요하므로 O(n*n)의 시간복잡도가 된다.
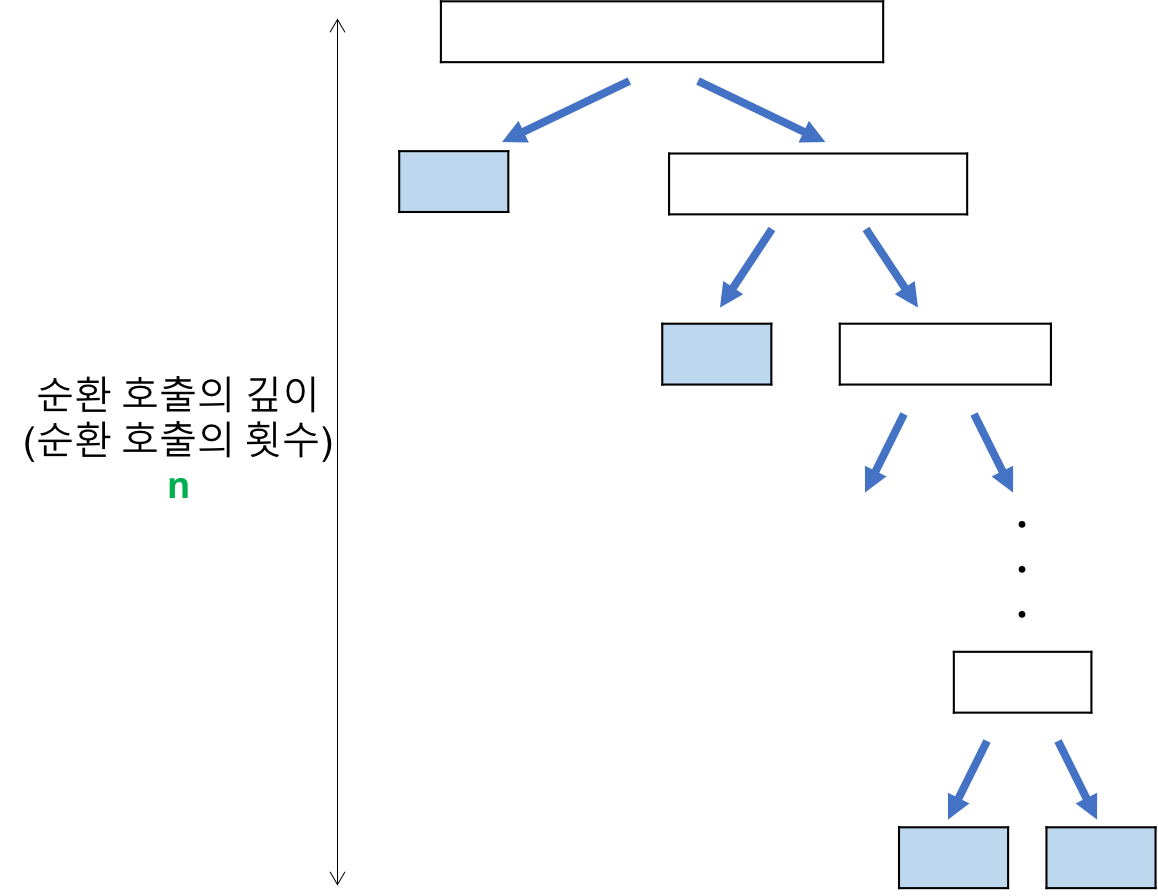
출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html 특히 다음과 같이 이미 정렬된 리스트에 대하여 퀵정렬을 실행하는 경우를 생각해보자.
이 경우 첫 번째 레코드를 피벗으로 설정하면, 다음과 같이 왼쪽 리스트가 텅 비게 되는 불균형 분할이 계속 된다.
1 2 3 4 5 6 7 8 9
1 (2 3 4 5 6 7 8 9)
1 2 (3 4 5 6 7 8 9)
. . .
1 2 3 4 5 6 7 8 9
그럼에도 불구하고 퀵 정렬은 평균적인 경우의 시간 복잡도가 O(nlog2n)으로 나타난다.
특히 O(nlog2n)의 복잡도를 가지는 다른 정렬 알고리즘과 비교하였을 때도 가장 빠른 것으로 나타났다. 이는 퀵정렬이 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한번 결정된 피벗들이 추후 연산에서 제외되는 특성이 있다.
퀵 정렬의 장단점
-
장점
-
속도가 빠르고 추가 메모리 공간을 필요로 하지 않는 등의 장점이 있다.
-
-
단점
-
정렬된 리스트에 대해서는 오히려 수행시간이 더 많이 걸린다.
-
이러한 불균형 분할을 방지하기 위하여 피벗을 선택할 때 단순히 리스트의 왼쪽 데이터를 사용하는 대신에 보다 리스트의 중앙 부분을 분할할 수 있는 데이터를 선택한다. 많이 사용되는 방법은 리스트 내의 몇개의 데이터 중에서 중간값을 피벗으로 선택하는 것이다.

출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html 반응형'Computer Science > Data_Structure' 카테고리의 다른 글
이진 탐색(Binary Search) 란? (0) 2020.01.30 힙 정렬(Heap sort) 란? (0) 2020.01.16 합병 정렬(merge sort) 란? (0) 2020.01.07 버블 정렬(bubble sort) 란? (0) 2020.01.07 삽입 정렬(insertion sort) 란? (0) 2020.01.07