힙 정렬(Heap sort) 란?

힙 정렬(Heap sort) 

힙 정렬은 최대 힙을 이용하면 가능하다. 예전에 힙(heap) 관련 글을 썼던 내용과 같이 보면 된다.

 

https://devlog-wjdrbs96.tistory.com/43?category=824010

힙(heap) 이란 ?

 

 

[5, 4, 2, 1, 7, 3, 9, 6, 3, 2] 배열이 존재한다고 가정할 때 데이터들을 차례대로 최대 힙에 삽입하여 아래와 같이 최대 힙 구조를 만든다. 

 

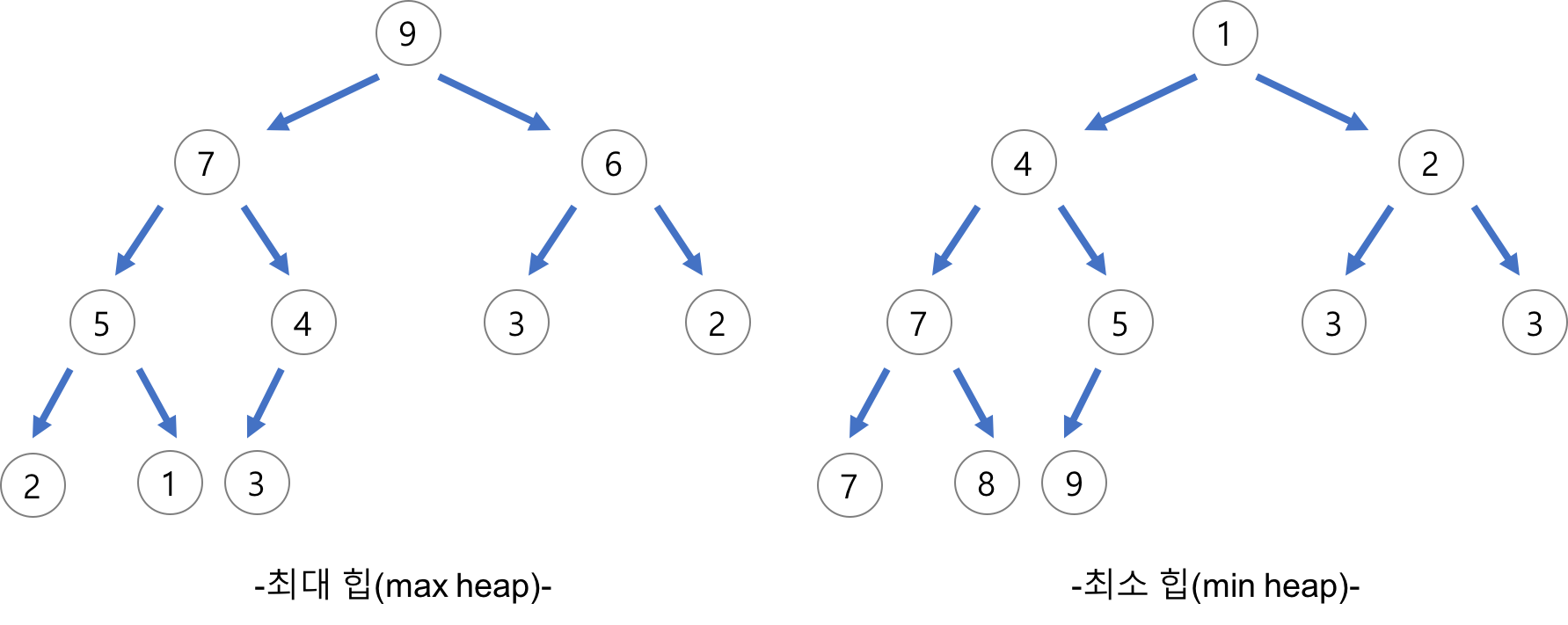
출처 : https://devlog-wjdrbs96.tistory.com/43?category=824010

 

 

그리고 나서 한번에 하나씩 요소를 히프에서 꺼내서 배열의 뒤쪽부터 저장하면 된다. 아니면 위의 배열의 데이터들을 최소 힙 구조를 만든 후에 하나씩 꺼내서 처음부터 저장해도 가능하다.

 

 

힙 정렬(Heap Sort) 구현

import java.util.ArrayList;
 
public class HeapSort {
    private ArrayList<Integer> heap;
 
    public HeapSort() {
        heap = new ArrayList<>();
        heap.add(0);  // 인덱스 0번은 버림
    }
 
    public void insert(int val) {
        heap.add(val);
        int p = heap.size()-1;
 
        while (p > 1 && heap.get(p / 2) < heap.get(p)) {
            int temp = heap.get(p / 2);
            heap.set(p/2, heap.get(p));
            heap.set(p, temp);
 
            p = p / 2;
        }
    }
 
    public int delete() {
        if (heap.size()-1 < 1) {
            return 0;
        }
 
        int deleteItem = heap.get(1);
        heap.set(1,heap.get(heap.size()-1));
        heap.remove(heap.size()-1);
 
        int parent = 1;
        int child = 2;
        while (child < heap.size()) {
            int max = heap.get(child);
 
            if (child < heap.size()-1 && max < heap.get(child + 1)) {
                max = heap.get(child + 1);
                child++;
            }
 
            if (heap.get(parent) > max) {
                break;
            }
 
            int temp = heap.get(parent);
            heap.set(parent, heap.get(child));
            heap.set(child, temp);
            parent = child;
            child+=2;
 
        }
        return deleteItem;
 
    }
 
    public static void main(String[] args) {
        int[] list = {5, 4, 2, 1, 7, 3, 9, 6, 3, 2};
        HeapSort heap = new HeapSort();
 
        for (int i =0; i < list.length; ++i) {
            heap.insert(list[i]);
        }
 
        for (int j = 0; j < list.length; ++j) {
            System.out.print(heap.delete() + " ");
        }
    }
}
 

 

 

 

힙 정렬 복잡도

• 힙 트리가 완전이진트리이므로 전체 높이가 거의 logN이다. 따라서 하나의 요소를 히프에 삽입하거나 삭제할 때 힙을 재정비하는 시간이 logN만큼 소요된다.
• 요소의 개수가 n개이므로 전체적으로 O(nlogN)의 시간이 걸린다.
• 힙 정렬은 최대로 유용한 경우는 전체자료를 정렬하는 것이 아니라 가장 큰 값 몇 개만 필요할 때이다. 

 

 

왜 삽입하거나 삭제할 때 힙을 재정비하는 시간이 logN 일까?

직관적으로 잘 이해가 가지는 않는다. 트리는 완전이진트리 이고 부모노드의 크기 > 자식노드의 크기 라는 규칙으로 만들어진 트리이다. 그렇기 때문에 삽입연산은 맨 마지막노드에 추가되어서 자기 자리를 찾아가고 삭제연산은 루트노드로 올라가서 자기 자리를 찾아가게 된다. 자기자리를 찾아가는 과정에서 삽입 연산일 때는 부모노드와 비교를 할 것이고 삭제연산일 때는 자식노드와 비교를 하게될 것이다. 이런 과정을 겪기 때문에 logN이라고 생각한다. 뭐 나도 시간복잡도에 대해서는 직관적으로 이해가 잘 되지는 않기 때문에 이 부분은 더 공부를 해야겠다.