이진 탐색(Binary Search) 란?

정렬된 배열에서의 이진 탐색 

정렬된 배열의 탐색에는 이진 탐색(binary search)이 가장 적합하다. 이진 탐색은 배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지를 알아내어 탐색의 범위를 반으로 줄인다.

이러한 방법에 의해 매 단계에서 검색해야 할 배열의 크기를 반으로 줄인다. 10억명의 정렬된 배열에서 이진 탐색을 이용하여 특정한 이름을 찾기 위해서는 단지 30번만 비교하면 된다. 

 

 

 

 

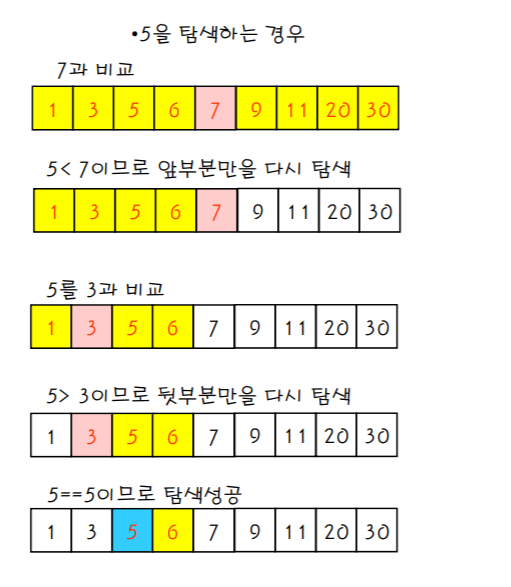
분할 정복 알고리즘과 이진 탐색

• 분할 정복 알고리즘 (Divide and Conquer)
  • Divide: 문제를 하나 또는 둘 이상으로 나눈다.
  • Conquer: 나눠진 문제가 충분히 작고, 해결이 가능하다면 해결하고, 그렇지 않다면 다시 나눈다.
• 이진 탐색
  • Divide: 리스트를 두 개의 서브 리스트로 나눈다.
  • Conquer
    
    • 검색할 숫자 (search) > 중간값 이면, 뒷 부분의 서브 리스트에서 검색할 숫자를 찾는다.
    • 검색할 숫자 (search) < 중간값 이면, 앞 부분의 서브 리스트에서 검색할 숫자를 찾는다.

 

 

 

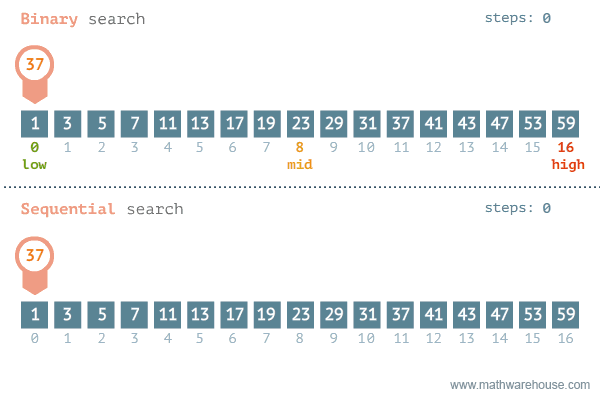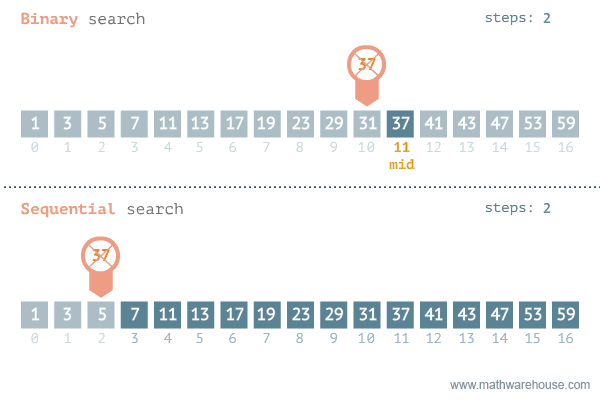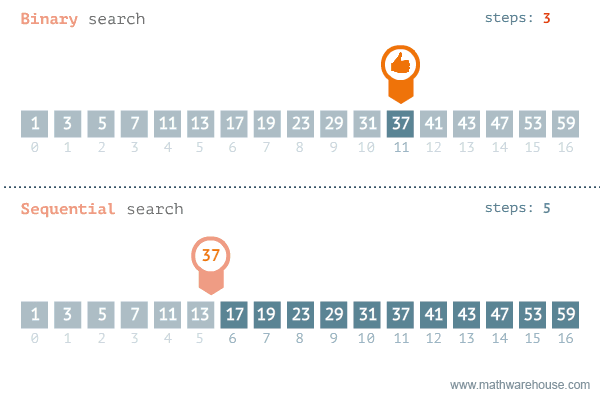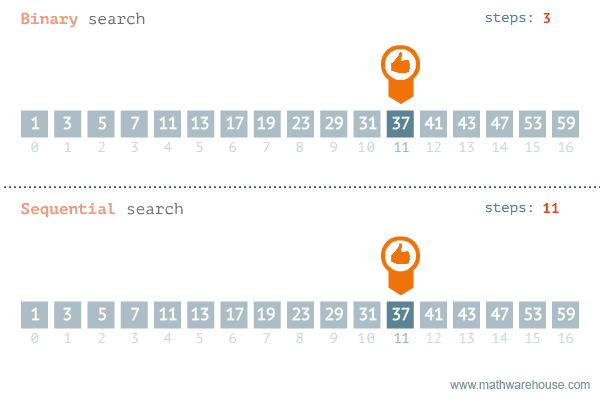
[저작자] by penjee.com&nbsp; 이미지 출처

이처럼 이진탐색과 순차탐색을 비교해보면 차이가 대략적으로 느낄 수 있다. 

 

 

 

이진 탐색(Binary Search) 특징 

이진 탐색에서는 비교가 이루어질 때마다 탐색 범위가 급격하게 줄어든다. 찾고자하는 항목이 속해있지 않은 부분은 전혀 고려할 필요가 없기 때문이다. 이진 탐색을 적용하려면 탐색하기 전에 배열이 반드시 정렬되어 있어야 한다. 따라서 이진 탐색은 데이터의 삽입이나 삭제가 빈번할 시에는 적합하지 않고, 주로 고정된 데이터에 대한 탐색에 적합하다.

 

 

 

 

이진 탐색(Binary Search) 구현 (순환 호출)

public class BinarySearch {
    static int[] list = {1, 3, 5, 6, 7, 9, 11, 20, 30};
    public static void main(String[] args) {
        System.out.println(Binary_Search(5, 0, list.length - 1));
        // 해당 값의 인덱스를 return, 없으면 -1 return
    }
 
    public static int Binary_Search(int key, int left, int right) {
        int mid;
 
        if (left <= right) {
            mid = (left + right) / 2;
            if (key == list[mid]) return mid;
 
            else if (key > list[mid]) {
                return Binary_Search(key, mid + 1, right);
            }
 
            else {
                return Binary_Search(key, left, mid - 1);
            }
        }
 
        return -1;
    }
}
 

 

 

이진 탐색(Binary Search) 시간복잡도 분석

배열의 개수를 n이라고 할 때, 이진 탐색은 n이 1이 될 때 까지 반복한다. 따라서 위의 식처럼 진행되면 k = log2n이 되기 때문에 시간복잡도는 O(logn)이 된다.