-
Kruskal 알고리즘이란?Computer Science/Algorithm 2020. 1. 23. 22:11728x90반응형
Kruskal 알고리즘
Kruskal의 알고리즘은 탐욕적인 방법(greedy method)을 이용한다. 탐욕적인 방법은 알고리즘 설계에서 있어서 중요한 기법 중의 하나이다. 탐욕적인 방법이란 선택할 때마다 그 순간 가장 좋았다고 생각되는 것을 선택함으로써 최종적인 해답에 도달하는 방법이다.
탐욕적인 알고리즘에서 순간의 선택은 그 당시에는 최적이다. 하지만 최적이라고 생각했던 지역적인 해답들을 모아서 최종적인 해답을 만들었다고 해서, 그 해답이 반드시 지역적으로 최적이라는 보장은 없다. 하지만 다행히 Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명되어 있다.
Kruskal의 알고리즘은 최소 비용 신장 트리가 최소 비용의 간선으로 구성됨과 동시에 사이클을 포함하지 않는다는 조건에 근거하여, 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택한다. 이러한 과정을 반복함으로써 네트워크의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구할 수 있다.
- Kruskal의 알고리즘은 먼저 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
- 정렬된 간선들의 리스트에서 사이클을 형성하지 않는 간선을 찾아서 현재의 최소 비용 신장 트리의 집합에 추가한다.
- 만약 사이클을 형성하면 그 간선은 제외한다.

출처 : https://gmlwjd9405.github.io/2018/08/29/algorithm-kruskal-mst.html Kruskal의 알고리즘을 이용하여 최소 비용 신장 트리를 만드는 과정을 보여준다. (a, f)가 가중치 10으로서 가장 낮기 때문에 먼저 선택되고 그 다음에 작은 순서대로 선택이 된다. 계속 진행되다 보면 (6)에서 (d, g)는 사이클이 형성 되기 때문에 제외되는 것을 확인할 수 있다. 유의할점은 다음 간선을 이미 선택된 간선들의 집합에 추가할 때 사이클을 생성하는 지를 체크하여야 한다.
이제 아래의 Kruskal 알고리즘을 그림을 통해 이해해보자.

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 위의 그래프를 살펴 보았을 때 노드는 7개이고, 간선의 개수는 11개 이다.
Kruskal 알고리즘은 위에서 설명한 순서대로 진행이 된다.
▷즉 사이클 테이블을 통해 두 점이 연결되어 있는지 여부를 파악한다. (Union-Find 알고리즘 이용한다)
▷최소비용 신장 트리에서는 사이클이 발생되면 안되기 때문이다.

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 위의 그림의 의미는 설명하자면, 맨 위의 (1, 7)는 노드의 번호고 그 아래 써져있는 12의 의미는 가중치의 의미이다. 위와 같은 형태로 그래프를 만들겠다는 의미이다.

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 위에 그림은 이미 가중치를 기준으로 오름차순으로 정렬한 상태이다. 이제 위에서 말했던 Kruskal 알고리즘의 순서대로 진행을 해보자.
- 위의 그래프를 가중치를 기준으로 오름차순으로 정렬한다.
- Union하기 전에 사이클 테이블을 확인한다.
- 사이클이 존재한다면 그 간선은 제외시킨다.

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 여기서 가장 쉽지 않은 것은 사이클 발생여부를 판단하는 것이다. 자세한 것은 Union-find글에서 다루도록 하겠다.
그리고 <사이클 테이블>은 배열로 구성하여 인덱스 = 현재노드번호, 배열안의 값은 해당 노드(인덱스)의 부모 노드의 번호를 의미한다. 초기 상태의 사이클 테이블은 자기 자신을 가리킨다.

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 위의 그림에서 가중치가 가장 낮은 12이고 간선 (1, 7)을 선택한다. 그러면 노드 7과 1이 연결이 되고 사이클 테이블에는 더 작은 값인 1이 부모가 된다.
두번 째로 다음으로 작은 가중치의 간선을 선택한다.

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 이것도 또한 (4, 7)의 간선이 선택되는데 일반적으로 부모는 작은 쪽으로 합치게 된다. union의 과정을 거치게 된다. 따라서 노드4의 부모도 1 - 4 - 7이 연결되어 있기 때문에 1이된다.
https://devlog-wjdrbs96.tistory.com/9
union 하는 과정은 위 블로그에서 자세히 공부하자.
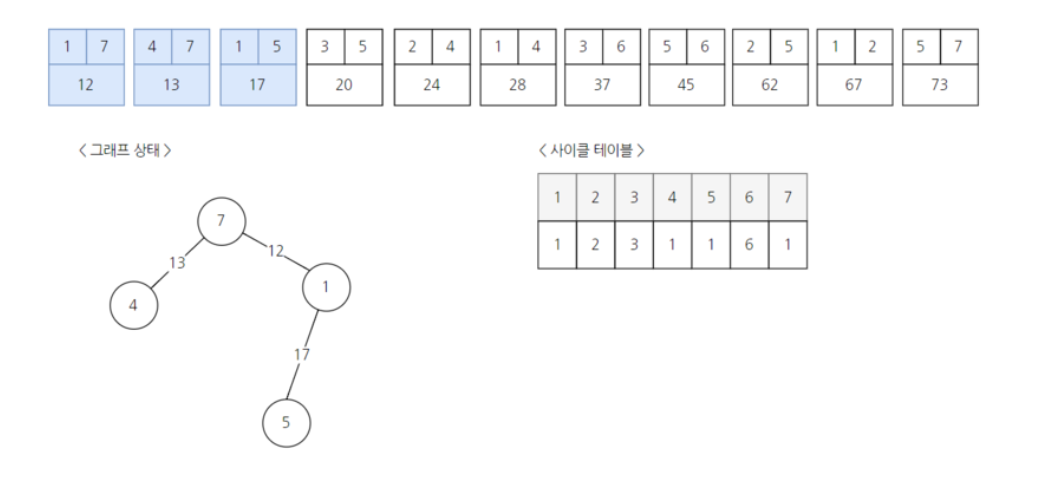
출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 세번 째로 작은 가중치의 간선인 (1, 5)를 연결한다. 따라서 5의 부모도 1이 된다.
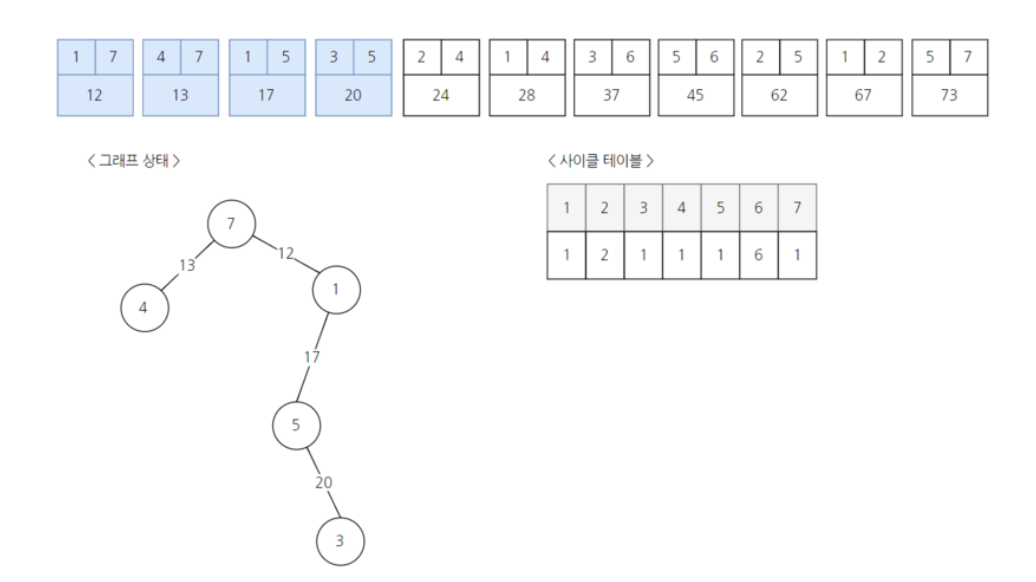
출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 다음에도 같은 원리로 진행된다.

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 다음에도 계속 똑같이 진행된다.
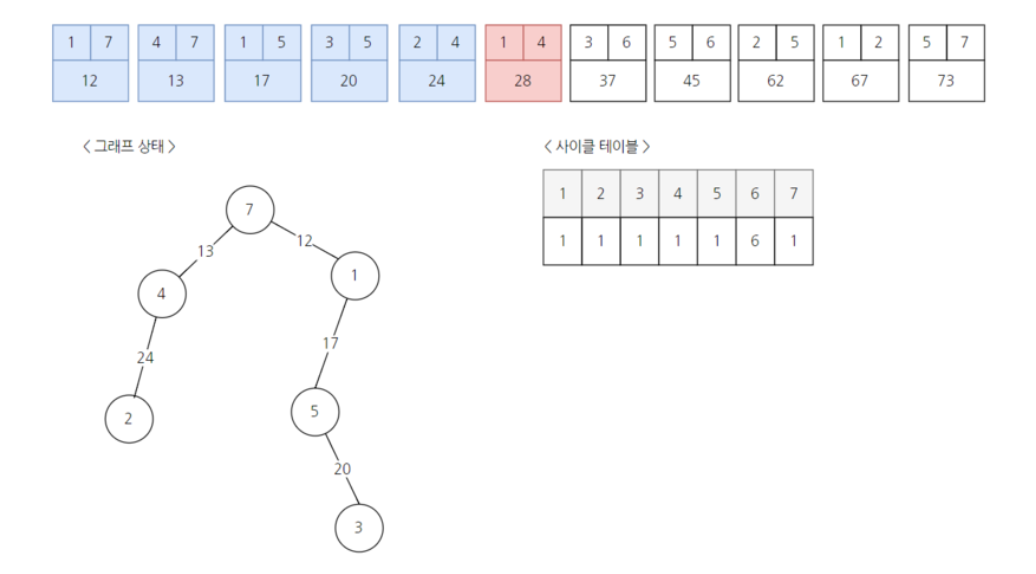
출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 하지만 이번에는 간선 (1, 4)를 추가하면 1 - 4 - 7 의 사이클이 생기기 때문에 추가할 수 없다. 따라서 (1, 4)의 간선은 제외하고 진행한다.
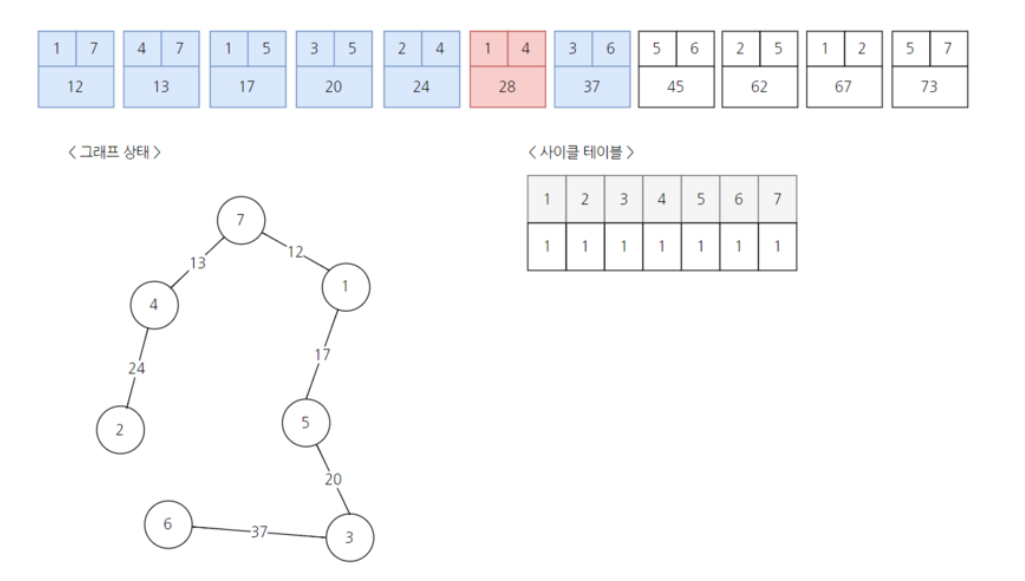
출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 그 다음에도 똑같이 사이클 여부를 확인하고 추가한다.

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221230994142&proxyReferer=https%3A%2F%2Fwww.google.com%2F 그 다음 나머지들은 전부 사이클이 생기기 때문에 추가할 수 없다. 따라서 이렇게 최소 비용 신장 트리가 완성되었다.
나는 개념은 쉬운데 뭔가 <사이클 테이블>에서 부모노드를 바꾸는 것이 살짝 헷갈렸다. 구현은 좀 더 쉽지 않았다.
Kruskal 알고리즘 with Java
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697import java.util.ArrayList;import java.util.Collections;class Edge implements Comparable<Edge> {int v1;int v2;int cost;Edge(int v1, int v2, int cost) {this.v1 = v1;this.v2 = v2;this.cost = cost;}@Overridepublic int compareTo(Edge o) { // cost를 가지고 정렬을 하겠다고 기준을 만듬if (this.cost < o.cost) {return - 1;}else if (this.cost == o.cost) {return 0;}else {return 1;}}}public class Kruskal {public static int[] parent;public static ArrayList<Edge> edgeList;public static void union(int x, int y) {x = find(x);y = find(y);if (x != y) {parent[y] = x;}}public static int find(int x) { // 부모 노드 찾는 메소드if (parent[x] == x) {return x;}return parent[x] = find(parent[x]);}public static boolean isSameParent(int x, int y) {x = find(x); // find 메소드를 통해서 부모 노드 번호를 리턴 받음y = find(y);if (x == y) {return true;}else {return false;}}public static void main(String[] args) {edgeList = new ArrayList<Edge>();edgeList.add(new Edge(1, 7, 12));edgeList.add(new Edge(1, 4, 28));edgeList.add(new Edge(1, 2, 67));edgeList.add(new Edge(1, 5, 17));edgeList.add(new Edge(2, 4, 24));edgeList.add(new Edge(2, 5, 62));edgeList.add(new Edge(3, 5, 20));edgeList.add(new Edge(3, 6, 37));edgeList.add(new Edge(4, 7, 13));edgeList.add(new Edge(5, 6, 45));edgeList.add(new Edge(5, 7, 73));parent = new int[8];for (int i = 1; i <= 7; ++i) {parent[i] = i;}Collections.sort(edgeList);int sum = 0;for (int i = 0; i < edgeList.size(); ++i) {Edge edge = edgeList.get(i);if(!isSameParent(edge.v1, edge.v2)) {sum += edge.cost;union(edge.v1, edge.v2);}}System.out.println(sum);}}[참고] (동빈나님 블로그에서 사진을 대부분 가져왔습니다)
18. 크루스칼 알고리즘(Kruskal Algorithm)
이번 시간에 다루어 볼 내용은 바로 크루스칼 알고리즘입니다. 크루스칼 알고리즘은 가장 적은 비용으로 모...
blog.naver.com
[참고]
https://gmlwjd9405.github.io/2018/08/29/algorithm-kruskal-mst.html
[알고리즘] Kruskal 알고리즘 이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
[참고]
https://brenden.tistory.com/36
[알고리즘] 크루스칼 알고리즘(Kruskal Algorithm)
크루스칼 알고리즘 (Kruskal Algorithm) ① 크루스칼 알고리즘이란? ▷ 최소 비용 신장 트리를 찾는 알고리즘입니다. ▷ 가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘입니다. ▷ 최소 스패닝..
brenden.tistory.com
반응형'Computer Science > Algorithm' 카테고리의 다른 글
동적 계획법 (Dynamic Programming)이란? (0) 2020.01.28 Dijkstra의 최단 경로 알고리즘이란? (0) 2020.01.28 Prim 알고리즘 이란? (0) 2020.01.27 Union-Find(합집합 찾기)란? (0) 2020.01.23 최소 비용 신장트리(MST, Minimum Spanning Tree)란? (0) 2020.01.23