레드블랙트리(Red-Black-Tree)란?

https://devlog-wjdrbs96.tistory.com/42?category=824010

이진 탐색 트리(binary search tree) 란?

기본적으로 레드블랙트리를 알기 위해서는 이진탐색트리가 무엇인지 알고 있어야 한다. 따라서 잘 모른다면 위의 글을 먼저 읽어보는 것을 추천하고, 안다는 가정하에 글을 써보려 한다. 

 

 

 

이진 탐색 트리의 분석

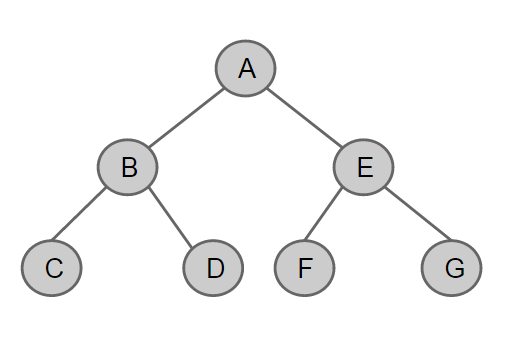
위와 같은 이진탐색트리 연산은 트리의 높이가 log2n이기 때문에 평균적인 경우의 시간복잡도는 O(log2h)이다.

그런데 만약 위처럼 균형잡힌 트리가 아니라 아래처럼 한쪽으로 치우치는 경사 트리가 되면 어떻게 될까? 

 

 

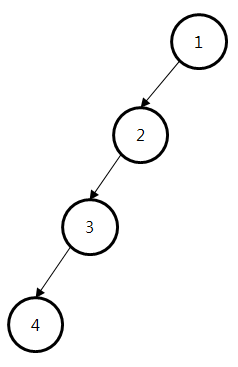
 그러면 트리의 높이가 n이 되기 때문에 탐색, 삽입, 삭제연산이 거의 선형 탐색과 같게 O(n)이 되기 때문에 트리의 장점이 사라지게 된다. 따라서 레드블랙트리는 이진탐색트리이지만, 노드를 삽입할 때 특정 조건이 존재하기 때문에 균형잡힌 트리로 만들어주는 역할을 한다. 

 

 

 

레드블랙트리의 조건

위에서 말한 것처럼 레드블랙트리를 만들어 균형잡힌 트리를 만들기 위해서는 어떤 조건이 필요하다. 

 

 

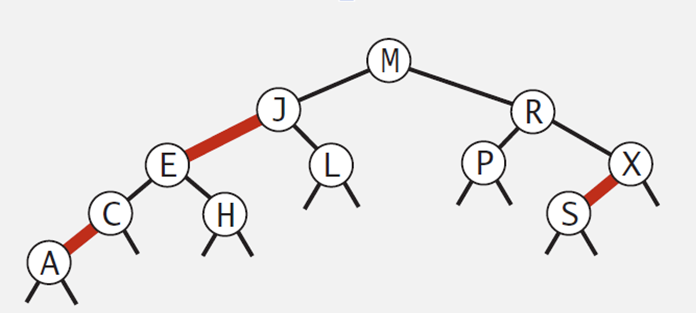
• 노드가 삽입될 때는 무조건 레드를 갖고 삽입하게 된다.
• 원래 일반적으로는 해당 노드에 색깔을 칠해주지만 이번에는 빨간색에 해당하는 노드와 부모노드와의 간선을 빨간색으로 칠해서 정의하려 한다. => 이와 같이 색깔(Color)필드를 갖는다.
• 모든 레드 링크는 왼쪽에만 존재해야 한다. (오른쪽 방향에 레드 링크가 존재해서는 안된다)
• 임의의 경로에서 레드 링크는 연속으로 연결되지 않아야 한다.(예를들어 J - E는 레드인데 E - C도 레드가 되면 안된다)
• 루트로부터 잎노드에 이르는 모든 경로상의 블랙 링크의 수는 모두 동일하다.
• Binary Search Tree와 동일한 검색 알고리즘을 사용하고 BST의 형태를 유지한다.

 

일반적인 이진탐색트리와 같이 삽입을 진행하는데 레드블랙트리는 무조건 노드가 삽입되게 되면 색깔은 레드(RED)이다.

그러면 아래와 같은 상황을 생각해보면서 좀 더 이해해보자.

 

• 오른쪽 자식이 레드이고, 왼쪽 자신이 블랙이라면? => Rotate Left (왼쪽 회전)
• 왼쪽자식의 색깔이 레드이고, 그 자식의 색깔도 레드라면? => Rotate Right (오른쪽 회전)
• 왼쪽자식과 오른쪽 자식이 모두 레드라면? => Flip Color (색깔반전) 

 

 

왼쪽 회전(Left Rotation : LR)

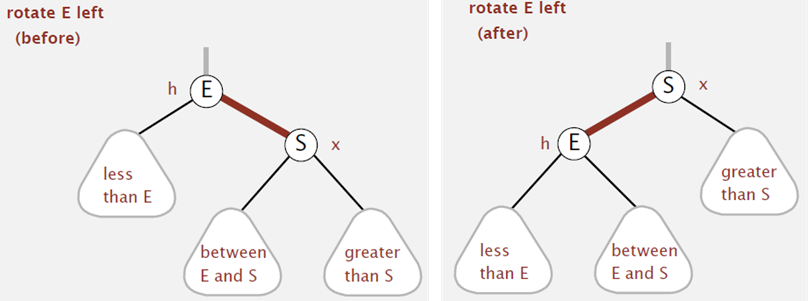
위의 사진에서 처럼 노드(E)의 오른쪽 자식노드(S)가 레드이기 때문에 위의 조건에 어긋나기 때문에 회전을 시켜줘야 한다. 이때 왼쪽회전을 시켜주면 되는데 말 그대로 왼쪽회전 = 반시계방향으로 생각해서 E를 반시계로 돌리면 S가 루트노드가 되어 오른쪽 그림처럼 회전이 된다.

 

 

오른쪽 회전(Right Rotation : RR)

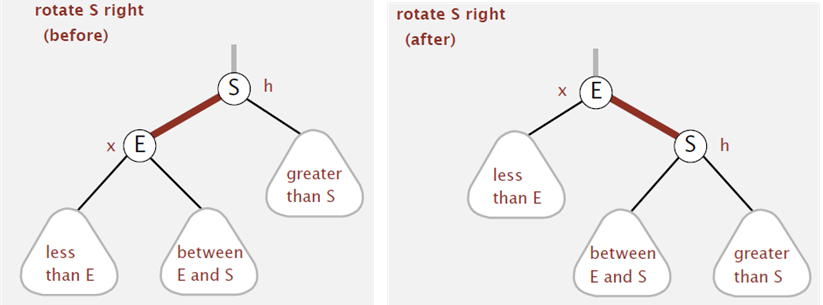
지금 위의 그림에서는 E의 왼쪽자식에 해당하는 부분이 빨간색이 존재하지 않지만 있다고 생각하고 빨간노드가 연속으로 2번 왔다고 생각하자. 이런 경우에는 오른쪽회전 = 시계방향으로 돌려서 회전시키면 된다. 따라서 S를 기준으로 오른쪽으로 돌리게 되면 E가 루트가 되고 S는 E의 오른쪽 자식이 된다. 오른쪽 사진에서는 실제로는 E의 왼쪽 자식과 오른쪽 자식이 둘다 레드이기 때문에 조건에 위배가 되지만 그 부분은 아래서 설명하려 한다.

 

 

색깔 반전(Color Flip : CF)

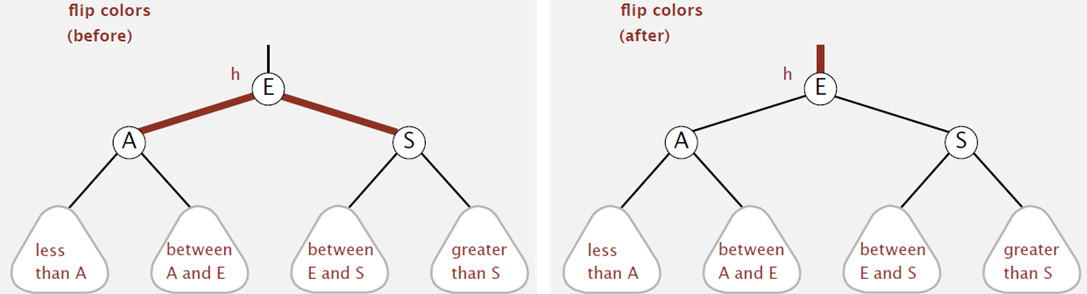
위와 같이 왼쪽자식과 오른쪽자식이 모두 레드에 해당할 때는 양쪽 자식의 노드를 블랙으로 바꾸고 루트노드의 색깔을 레드에서 블랙으로 바꾸게 되어 색깔반전이라고 한다. 

 

 

 

그럼 이번에는 SEARCHXMPL을 순서대로 레드블랙트리의 조건에 맞춰 삽입해보자.

가장처음에 S가 삽입되어 루트에 들어가게 될 것이고, E가 삽입되었을 때는 S보다 작은 값이기 때문에 S의 왼쪽자식으로 레드로 들어가게 된다 (이유는 위에를 참고) 

 

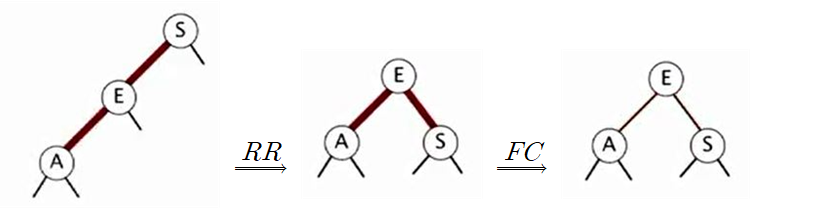
그리고 A도 삽입하게 되면 위와 같이 경사트리가 만들어지게 되고 레드 - 레드가 2번 연속으로 나왔기 때문에 조건에 위배되어 Right Rotation(RR)을 통해서 중간그림에 있는 트리처럼 만들고 이번에는 양쪽다 레드이기 때문에 Flip Color를 통해서 색깔을 반전시켜준다.

 

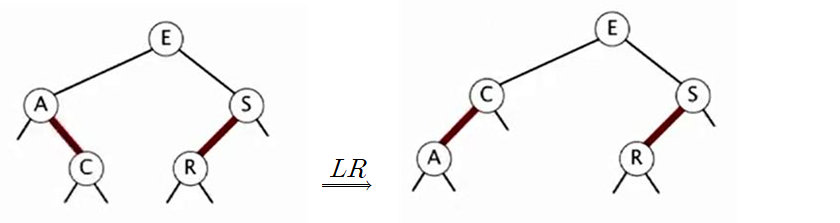
R은 S의 왼쪽자식으로 삽압이 된 상태고 그 다음에 C가 삽입이 되어 A의 오른쪽 자식으로 들어갔는데 이게 레드이기 때문에 조건에 위배가 되어 Left Rotation(LR)을 진행하여 오른쪽 트리가 완성된 상태이다. 

 

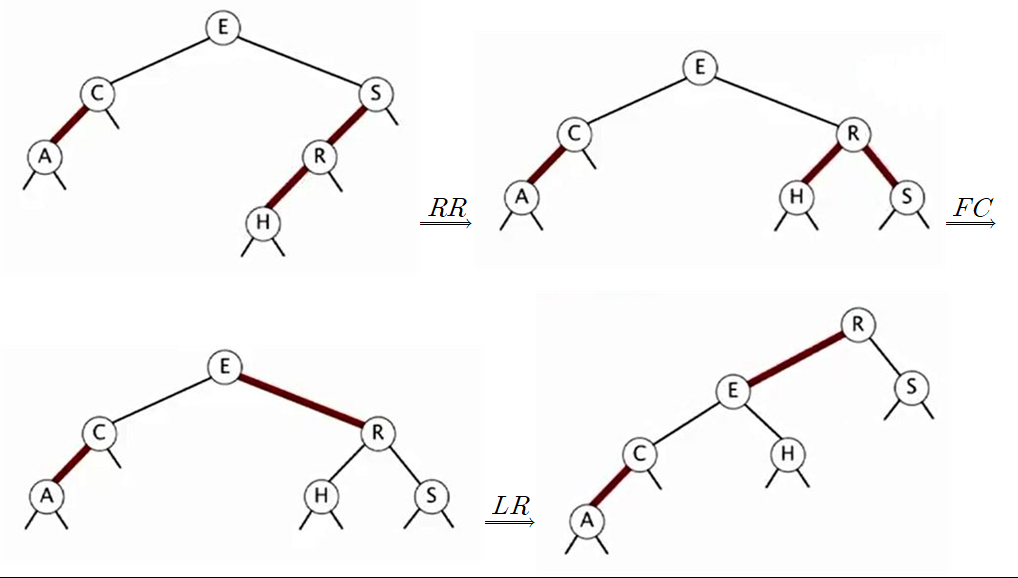
그리고 H가 삽입이 된 경우인데 이 때는 레드가 연속으로 2번 나왔기 때문에 RR을 진행하고 그 다음에는 R의 왼쪽자식과 오른쪽 자식이 레드이기 때문에 Flip Color를 통해서 색깔 반전을 시킨다. 그리고 마지막으로 R이 오른쪽 자식이지만 레드이기 때문에 조건에 위배가 되어 LR을 적용하여 오른쪽 아래의 그림처럼 트리가 완성이 된다.

 

 

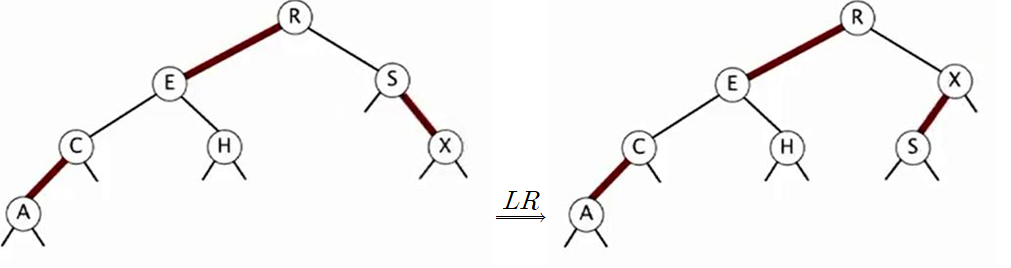
위에는 X를 삽입한 상황인데 계속 위에서 설명한 내용과 같기 때문에 조건에 위배될 때 마다 적용해주면 된다.

 

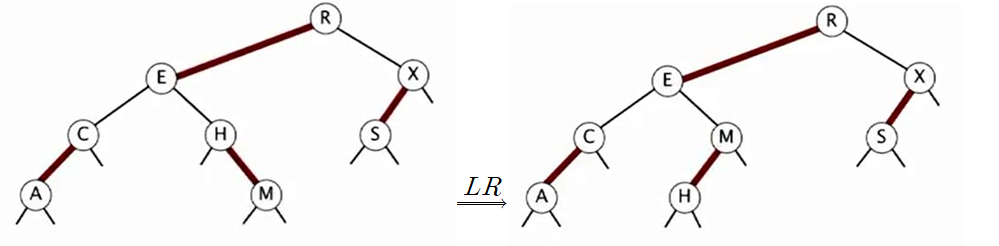
이번에는 M이 삽입된 상황이다.

 

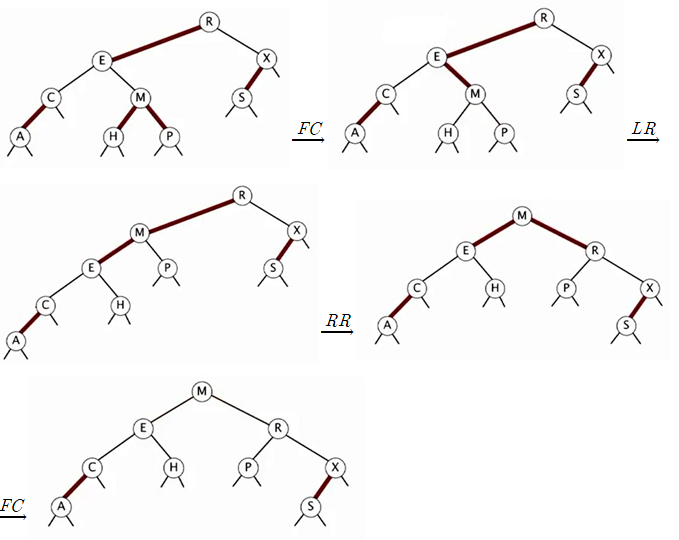
이번에는 P를 삽입한 상황인데 이 경우는 조금 복잡하다. 따라서 그림으로 보면 그러려니 해도 그림 없이 스스로 생각해서 하려고 하면 헷갈리고 한번 실수하면 다시 해야 하기 때문에 머리 아프고 어렵지만 차근차근 해보길 바란다.

 

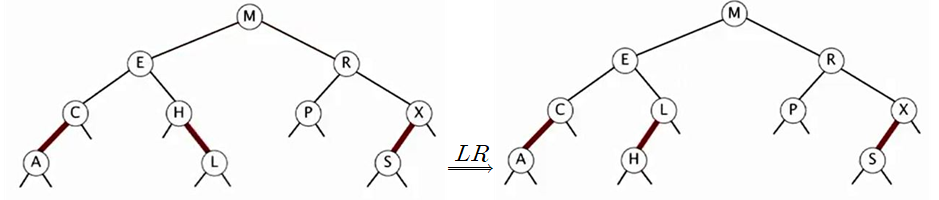
그리고 마지막 L이 삽입되어 최종 레드블랙트리가 완성된 모습을 볼 수 있다.

 

 

코드 구현(with Java)

public class RBT <K extends Comparable<K>, V> {

    private static final boolean RED = true;
    private static final boolean BLACK = false;

    private class Node {
        private K key;
        private V val;
        private Node left, right;
        private boolean color;

        public Node(K k, V v, boolean color) {
            this.key = k;
            this.val = v;
            this.color = color;
        }
    }

    private Node root;

    public RBT() {}

    private Node search(Node node, K k) {
        if (node == null) return null;
        int cmp = k.compareTo(node.key);
        if (cmp < 0) return search(node.left, k);
        else if (cmp > 0) return search(node.right, k);
        return node;
    }

    public Node search(K k) {
        return search(root, k);
    }

    private Node insert(Node node, K k, V v) {
        if (node == null) return new Node(k, v, RED);
        int cmp = k.compareTo(node.key);
        if (cmp < 0) node.left = insert(node.left, k, v);
        else if (cmp > 0) node.right = insert(node.right, k, v);
        else node.val = v;

        if (isRed(node.right) && !isRed(node.left)) {
            node = rotateLeft(node);
        }
        if (isRed(node.left) && isRed(node.left.left)) {
            node = rotateRight(node);
        }
        if (isRed(node.left) && isRed(node.right)) {
            flipColors(node);
        }

        return node;
    }

    public void insert(K k, V v) {
        root = insert(root, k, v);
        root.color = BLACK;
    }

    private Node rotateLeft(Node h) {
        Node x = h.right;
        h.right = x.left;
        x.left = h;
        x.color = h.color;
        h.color = RED;
        return x;
    }

    private Node rotateRight(Node h) {
        Node x = h.left;
        h.left = x.right;
        x.right = h;
        x.color = h.color;
        x.color = RED;
        return x;
    }

    private void flipColors(Node h) {
        h.color = RED;
        h.left.color = BLACK;
        h.right.color = BLACK;
    }

    private boolean isRed(Node x) {
        if (x == null) return false;
        return x.color == RED;
    }

    private void inorder(Node node) {
        if (node == null) return;
        inorder(node.left);
        System.out.print(node.key + " ");
        inorder(node.right);
    }

    public void inorder() {
        System.out.print("In-order : ");
        inorder(root);
        System.out.println();
    }

    private int height(Node node) {
        if (node == null) return -1;
        return 1 + Math.max(height(node.left), height(node.right));
    }

    public int height() {
        return height(root);
    }

    public K getRootKey() {
        return root.key;
    }

    public V getValue(Node node) {
        return node.val;
    }
}